Distributional Reinforcement Learning via Sinkhorn Iterations
Paper and Code
Feb 16, 2022
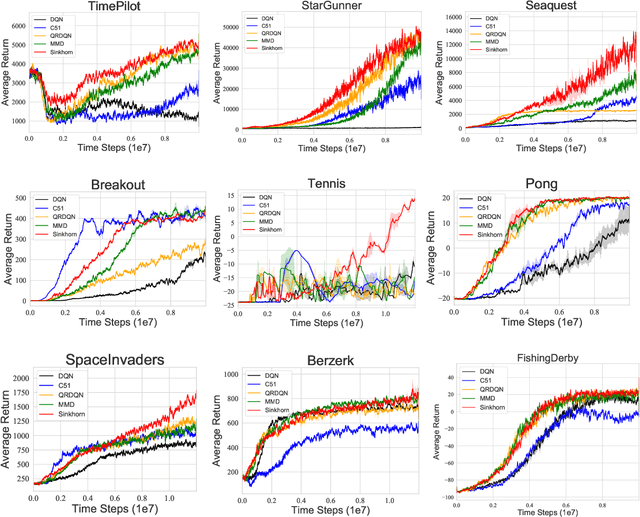
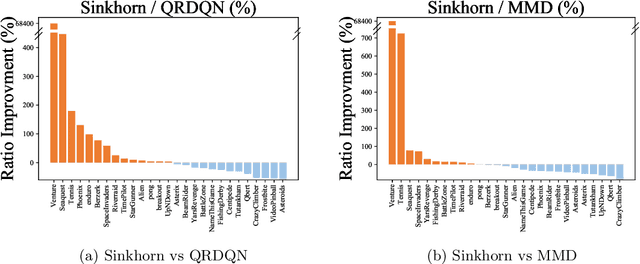
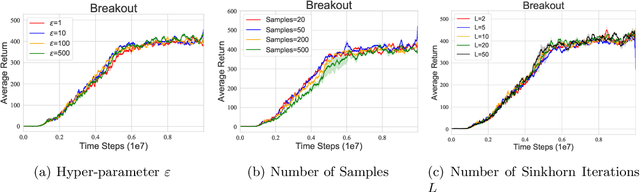
Distributional reinforcement learning~(RL) is a class of state-of-the-art algorithms that estimate the whole distribution of the total return rather than only its expectation. The representation manner of each return distribution and the choice of distribution divergence are pivotal for the empirical success of distributional RL. In this paper, we propose a new class of \textit{Sinkhorn distributional RL} algorithm that learns a finite set of statistics, i.e., deterministic samples, from each return distribution and then leverages Sinkhorn iterations to evaluate the Sinkhorn distance between the current and target Bellmen distributions. Remarkably, as Sinkhorn divergence interpolates between the Wasserstein distance and Maximum Mean Discrepancy~(MMD). This allows our proposed Sinkhorn distributional RL algorithms to find a sweet spot leveraging the geometry of optimal transport-based distance, and the unbiased gradient estimates of MMD. Finally, experiments on a suite of Atari games reveal the competitive performance of Sinkhorn distributional RL algorithm as opposed to existing state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge