Damped Anderson Mixing for Deep Reinforcement Learning: Acceleration, Convergence, and Stabilization
Paper and Code
Oct 20, 2021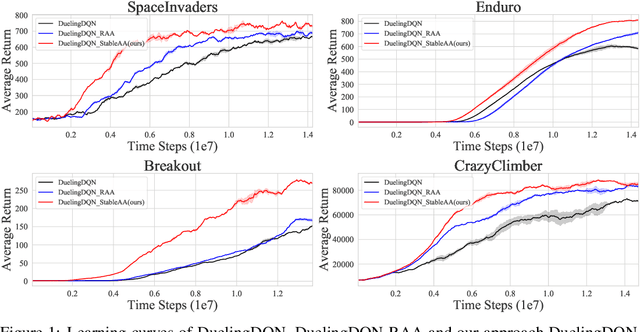
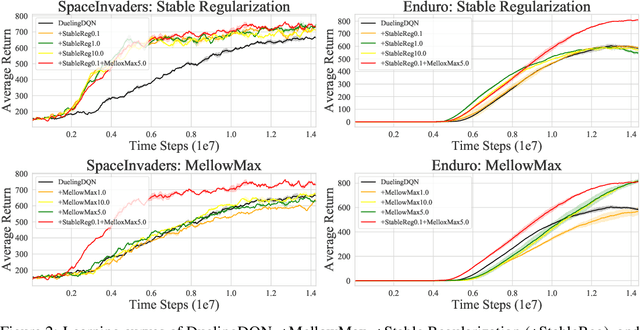
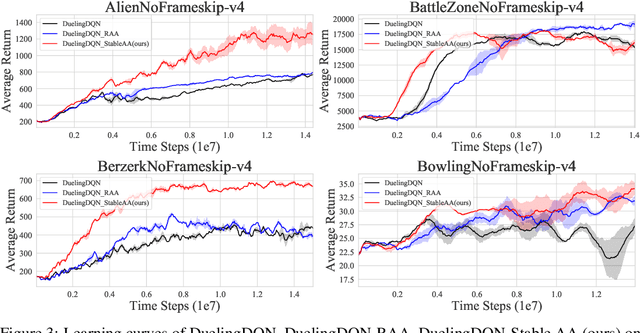
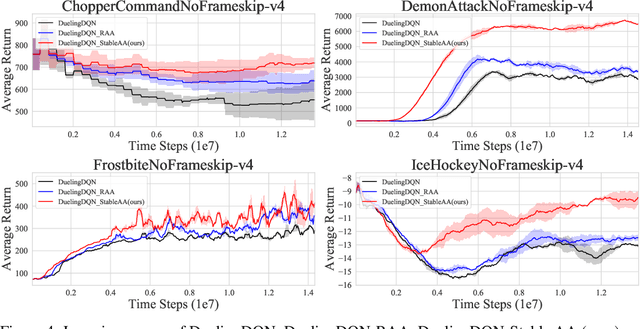
Anderson mixing has been heuristically applied to reinforcement learning (RL) algorithms for accelerating convergence and improving the sampling efficiency of deep RL. Despite its heuristic improvement of convergence, a rigorous mathematical justification for the benefits of Anderson mixing in RL has not yet been put forward. In this paper, we provide deeper insights into a class of acceleration schemes built on Anderson mixing that improve the convergence of deep RL algorithms. Our main results establish a connection between Anderson mixing and quasi-Newton methods and prove that Anderson mixing increases the convergence radius of policy iteration schemes by an extra contraction factor. The key focus of the analysis roots in the fixed-point iteration nature of RL. We further propose a stabilization strategy by introducing a stable regularization term in Anderson mixing and a differentiable, non-expansive MellowMax operator that can allow both faster convergence and more stable behavior. Extensive experiments demonstrate that our proposed method enhances the convergence, stability, and performance of RL algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge