Sparsity regularization via tree-structured environments for disentangled representations

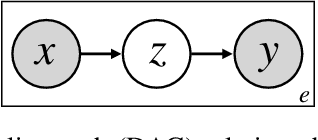
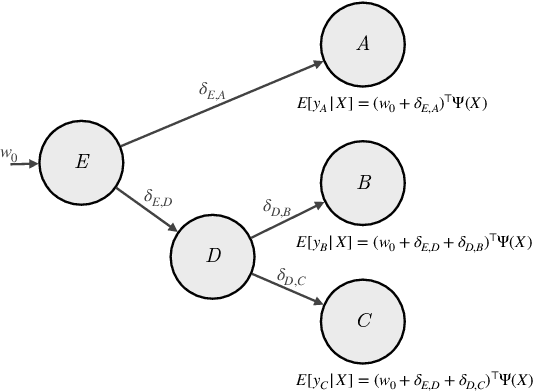
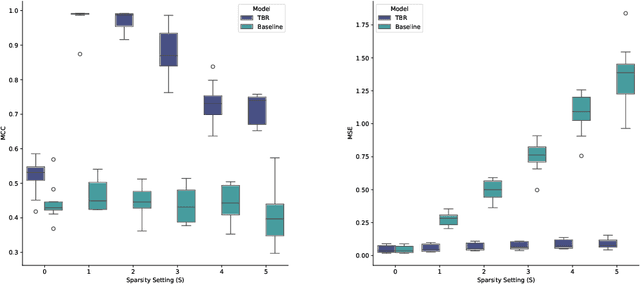
Many causal systems such as biological processes in cells can only be observed indirectly via measurements, such as gene expression. Causal representation learning -- the task of correctly mapping low-level observations to latent causal variables -- could advance scientific understanding by enabling inference of latent variables such as pathway activation. In this paper, we develop methods for inferring latent variables from multiple related datasets (environments) and tasks. As a running example, we consider the task of predicting a phenotype from gene expression, where we often collect data from multiple cell types or organisms that are related in known ways. The key insight is that the mapping from latent variables driven by gene expression to the phenotype of interest changes sparsely across closely related environments. To model sparse changes, we introduce Tree-Based Regularization (TBR), an objective that minimizes both prediction error and regularizes closely related environments to learn similar predictors. We prove that under assumptions about the degree of sparse changes, TBR identifies the true latent variables up to some simple transformations. We evaluate the theory empirically with both simulations and ground-truth gene expression data. We find that TBR recovers the latent causal variables better than related methods across these settings, even under settings that violate some assumptions of the theory.

Leveraging Structure Between Environments: Phylogenetic Regularization Incentivizes Disentangled Representations

Many causal systems such as biological processes in cells can only be observed indirectly via measurements, such as gene expression. Causal representation learning -- the task of correctly mapping low-level observations to latent causal variables -- could advance scientific understanding by enabling inference of latent variables such as pathway activation. In this paper, we develop methods for inferring latent variables from multiple related datasets (environments) and tasks. As a running example, we consider the task of predicting a phenotype from gene expression, where we often collect data from multiple cell types or organisms that are related in known ways. The key insight is that the mapping from latent variables driven by gene expression to the phenotype of interest changes sparsely across closely related environments. To model sparse changes, we introduce Tree-Based Regularization (TBR), an objective that minimizes both prediction error and regularizes closely related environments to learn similar predictors. We prove that under assumptions about the degree of sparse changes, TBR identifies the true latent variables up to some simple transformations. We evaluate the theory empirically with both simulations and ground-truth gene expression data. We find that TBR recovers the latent causal variables better than related methods across these settings, even under settings that violate some assumptions of the theory.

PhyloGFN: Phylogenetic inference with generative flow networks

Phylogenetics is a branch of computational biology that studies the evolutionary relationships among biological entities. Its long history and numerous applications notwithstanding, inference of phylogenetic trees from sequence data remains challenging: the high complexity of tree space poses a significant obstacle for the current combinatorial and probabilistic techniques. In this paper, we adopt the framework of generative flow networks (GFlowNets) to tackle two core problems in phylogenetics: parsimony-based and Bayesian phylogenetic inference. Because GFlowNets are well-suited for sampling complex combinatorial structures, they are a natural choice for exploring and sampling from the multimodal posterior distribution over tree topologies and evolutionary distances. We demonstrate that our amortized posterior sampler, PhyloGFN, produces diverse and high-quality evolutionary hypotheses on real benchmark datasets. PhyloGFN is competitive with prior works in marginal likelihood estimation and achieves a closer fit to the target distribution than state-of-the-art variational inference methods.