SNAP: Sequential Non-Ancestor Pruning for Targeted Causal Effect Estimation With an Unknown Graph

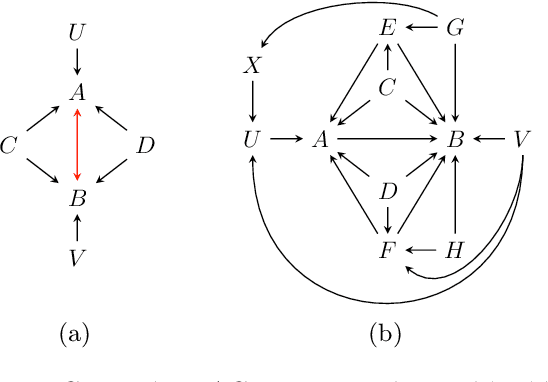
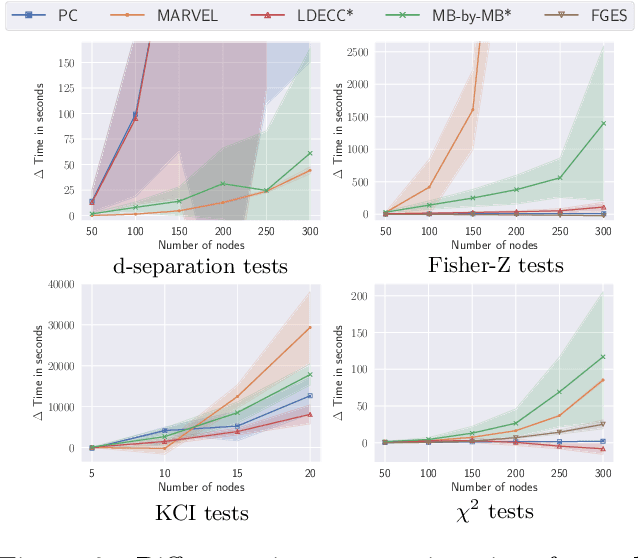
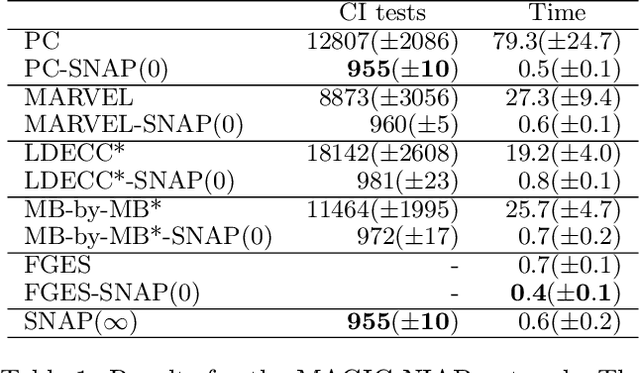
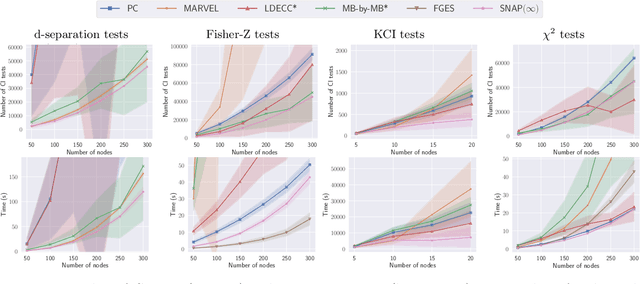
Causal discovery can be computationally demanding for large numbers of variables. If we only wish to estimate the causal effects on a small subset of target variables, we might not need to learn the causal graph for all variables, but only a small subgraph that includes the targets and their adjustment sets. In this paper, we focus on identifying causal effects between target variables in a computationally and statistically efficient way. This task combines causal discovery and effect estimation, aligning the discovery objective with the effects to be estimated. We show that definite non-ancestors of the targets are unnecessary to learn causal relations between the targets and to identify efficient adjustments sets. We sequentially identify and prune these definite non-ancestors with our Sequential Non-Ancestor Pruning (SNAP) framework, which can be used either as a preprocessing step to standard causal discovery methods, or as a standalone sound and complete causal discovery algorithm. Our results on synthetic and real data show that both approaches substantially reduce the number of independence tests and the computation time without compromising the quality of causal effect estimations.

Establishing Markov Equivalence in Cyclic Directed Graphs

We present a new, efficient procedure to establish Markov equivalence between directed graphs that may or may not contain cycles under the \textit{d}-separation criterion. It is based on the Cyclic Equivalence Theorem (CET) in the seminal works on cyclic models by Thomas Richardson in the mid '90s, but now rephrased from an ancestral perspective. The resulting characterization leads to a procedure for establishing Markov equivalence between graphs that no longer requires tests for d-separation, leading to a significantly reduced algorithmic complexity. The conceptually simplified characterization may help to reinvigorate theoretical research towards sound and complete cyclic discovery in the presence of latent confounders. This version includes a correction to rule (iv) in Theorem 1, and the subsequent adjustment in part 2 of Algorithm 2.

Towards a Benchmark for Scientific Understanding in Humans and Machines

Scientific understanding is a fundamental goal of science, allowing us to explain the world. There is currently no good way to measure the scientific understanding of agents, whether these be humans or Artificial Intelligence systems. Without a clear benchmark, it is challenging to evaluate and compare different levels of and approaches to scientific understanding. In this Roadmap, we propose a framework to create a benchmark for scientific understanding, utilizing tools from philosophy of science. We adopt a behavioral notion according to which genuine understanding should be recognized as an ability to perform certain tasks. We extend this notion by considering a set of questions that can gauge different levels of scientific understanding, covering information retrieval, the capability to arrange information to produce an explanation, and the ability to infer how things would be different under different circumstances. The Scientific Understanding Benchmark (SUB), which is formed by a set of these tests, allows for the evaluation and comparison of different approaches. Benchmarking plays a crucial role in establishing trust, ensuring quality control, and providing a basis for performance evaluation. By aligning machine and human scientific understanding we can improve their utility, ultimately advancing scientific understanding and helping to discover new insights within machines.

Inferring the Direction of a Causal Link and Estimating Its Effect via a Bayesian Mendelian Randomization Approach

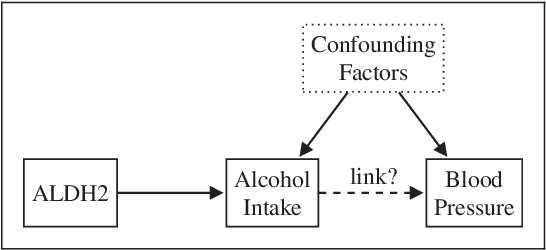
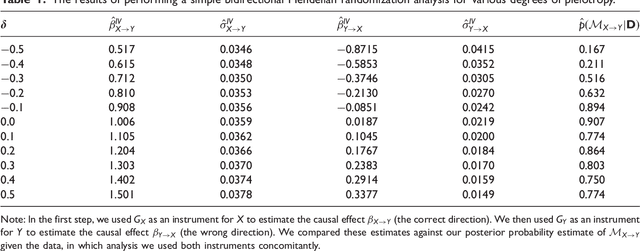
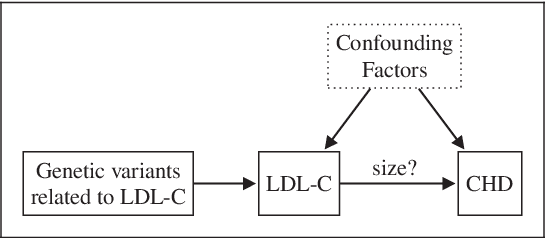
The use of genetic variants as instrumental variables - an approach known as Mendelian randomization - is a popular epidemiological method for estimating the causal effect of an exposure (phenotype, biomarker, risk factor) on a disease or health-related outcome from observational data. Instrumental variables must satisfy strong, often untestable assumptions, which means that finding good genetic instruments among a large list of potential candidates is challenging. This difficulty is compounded by the fact that many genetic variants influence more than one phenotype through different causal pathways, a phenomenon called horizontal pleiotropy. This leads to errors not only in estimating the magnitude of the causal effect but also in inferring the direction of the putative causal link. In this paper, we propose a Bayesian approach called BayesMR that is a generalization of the Mendelian randomization technique in which we allow for pleiotropic effects and, crucially, for the possibility of reverse causation. The output of the method is a posterior distribution over the target causal effect, which provides an immediate and easily interpretable measure of the uncertainty in the estimation. More importantly, we use Bayesian model averaging to determine how much more likely the inferred direction is relative to the reverse direction.

MASSIVE: Tractable and Robust Bayesian Learning of Many-Dimensional Instrumental Variable Models

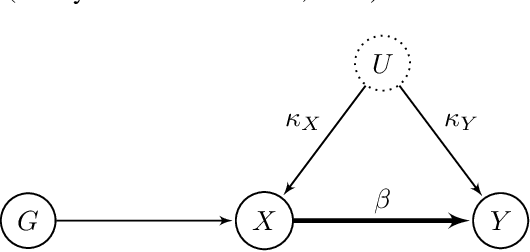
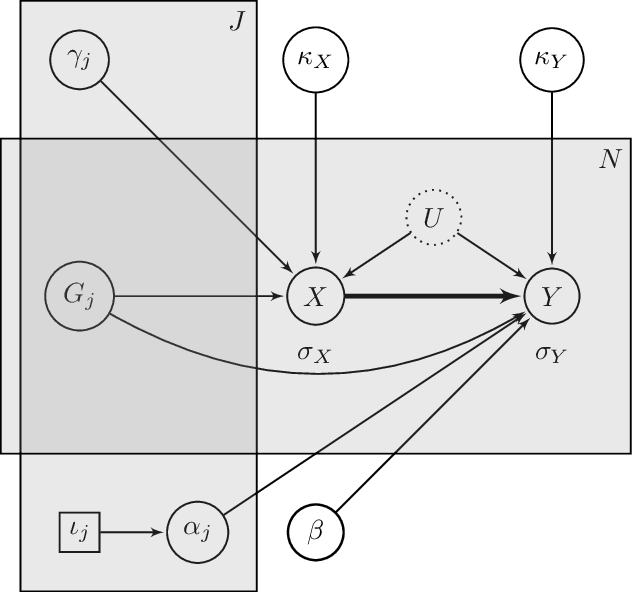
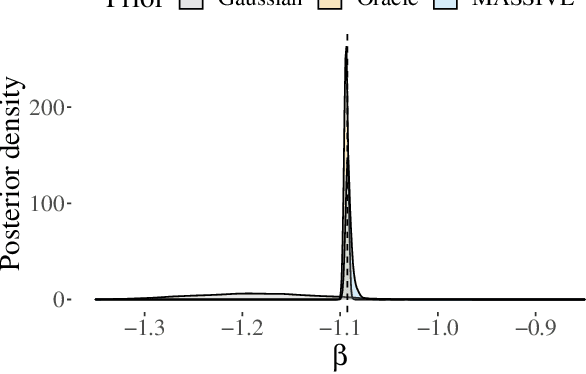
The recent availability of huge, many-dimensional data sets, like those arising from genome-wide association studies (GWAS), provides many opportunities for strengthening causal inference. One popular approach is to utilize these many-dimensional measurements as instrumental variables (instruments) for improving the causal effect estimate between other pairs of variables. Unfortunately, searching for proper instruments in a many-dimensional set of candidates is a daunting task due to the intractable model space and the fact that we cannot directly test which of these candidates are valid, so most existing search methods either rely on overly stringent modeling assumptions or fail to capture the inherent model uncertainty in the selection process. We show that, as long as at least some of the candidates are (close to) valid, without knowing a priori which ones, they collectively still pose enough restrictions on the target interaction to obtain a reliable causal effect estimate. We propose a general and efficient causal inference algorithm that accounts for model uncertainty by performing Bayesian model averaging over the most promising many-dimensional instrumental variable models, while at the same time employing weaker assumptions regarding the data generating process. We showcase the efficiency, robustness and predictive performance of our algorithm through experimental results on both simulated and real-world data.

Causal Shapley Values: Exploiting Causal Knowledge to Explain Individual Predictions of Complex Models

Shapley values underlie one of the most popular model-agnostic methods within explainable artificial intelligence. These values are designed to attribute the difference between a model's prediction and an average baseline to the different features used as input to the model. Being based on solid game-theoretic principles, Shapley values uniquely satisfy several desirable properties, which is why they are increasingly used to explain the predictions of possibly complex and highly non-linear machine learning models. Shapley values are well calibrated to a user's intuition when features are independent, but may lead to undesirable, counterintuitive explanations when the independence assumption is violated. In this paper, we propose a novel framework for computing Shapley values that generalizes recent work that aims to circumvent the independence assumption. By employing Pearl's do-calculus, we show how these 'causal' Shapley values can be derived for general causal graphs without sacrificing any of their desirable properties. Moreover, causal Shapley values enable us to separate the contribution of direct and indirect effects. We provide a practical implementation for computing causal Shapley values based on causal chain graphs when only partial information is available and illustrate their utility on a real-world example.

Constraint-Based Causal Discovery In The Presence Of Cycles

While feedback loops are known to play important roles in many complex systems (for example, in economical, biological, chemical, physical, control and climatological systems), their existence is ignored in most of the causal discovery literature, where systems are typically assumed to be acyclic from the outset. When applying causal discovery algorithms designed for the acyclic setting on data generated by a system that involves feedback, one would not expect to obtain correct results, even in the infinite-sample limit. In this work, we show that---surprisingly---the output of the Fast Causal Inference (FCI) algorithm is correct if it is applied to observational data generated by a system that involves feedback. More specifically, we prove that for observational data generated by a simple and $\sigma$-faithful Structural Causal Model (SCM), FCI can be used to consistently estimate (i) the presence and absence of causal relations, (ii) the presence and absence of direct causal relations, (iii) the absence of confounders, and (iv) the absence of specific cycles in the causal graph of the SCM.

Large-Scale Local Causal Inference of Gene Regulatory Relationships

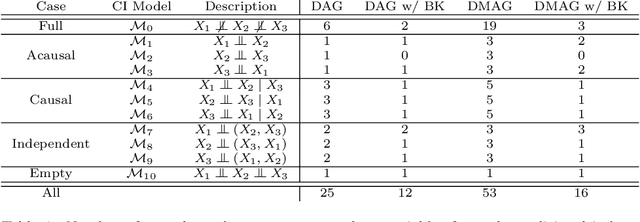
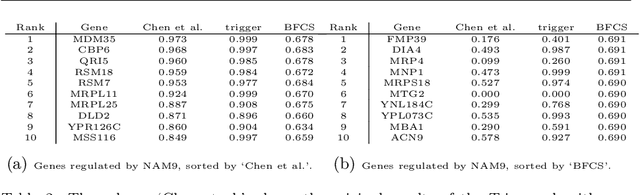
Gene regulatory networks play a crucial role in controlling an organism's biological processes, which is why there is significant interest in developing computational methods that are able to extract their structure from high-throughput genetic data. Many of these computational methods are designed to infer individual regulatory relationships among genes from data on gene expression. We propose a novel efficient Bayesian method for discovering local causal relationships among triplets of (normally distributed) variables. In our approach, we score covariance structures for each triplet in one go and incorporate available background knowledge in the form of priors to derive posterior probabilities over local causal structures. Our method is flexible in the sense that it allows for different types of causal structures and assumptions. We apply our approach to the task of learning causal regulatory relationships among genes. We show that the proposed algorithm produces stable and conservative posterior probability estimates over local causal structures that can be used to derive an honest ranking of the most meaningful regulatory relationships. We demonstrate the stability and efficacy of our method both on simulated data and on real-world data from an experiment on yeast.

Domain Adaptation by Using Causal Inference to Predict Invariant Conditional Distributions

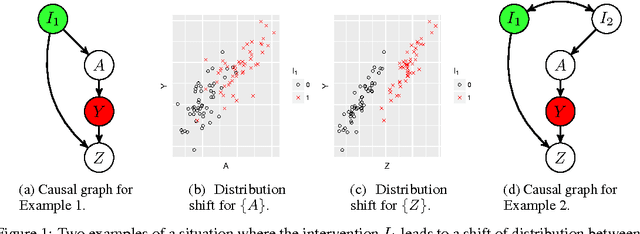
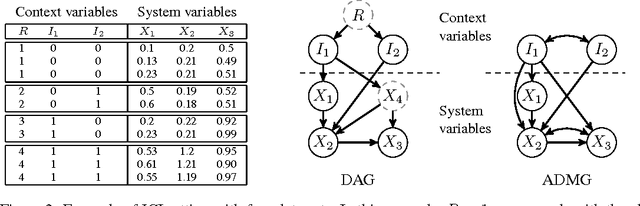
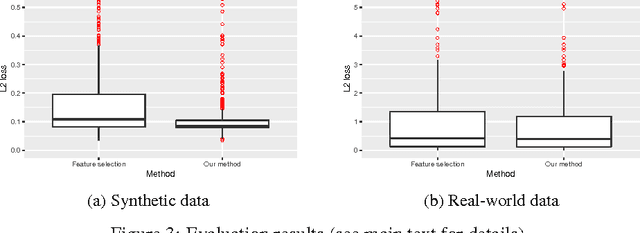
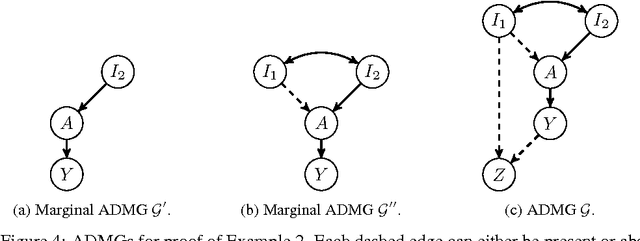
An important goal common to domain adaptation and causal inference is to make accurate predictions when the distributions for the source (or training) domain(s) and target (or test) domain(s) differ. In many cases, these different distributions can be modeled as different contexts of a single underlying system, in which each distribution corresponds to a different perturbation of the system, or in causal terms, an intervention. We focus on a class of such causal domain adaptation problems, where data for one or more source domains are given, and the task is to predict the distribution of a certain target variable from measurements of other variables in one or more target domains. We propose an approach for solving these problems that exploits causal inference and does not rely on prior knowledge of the causal graph, the type of interventions or the intervention targets. We demonstrate our approach by evaluating a possible implementation on simulated and real world data.

A Bayesian Approach for Inferring Local Causal Structure in Gene Regulatory Networks

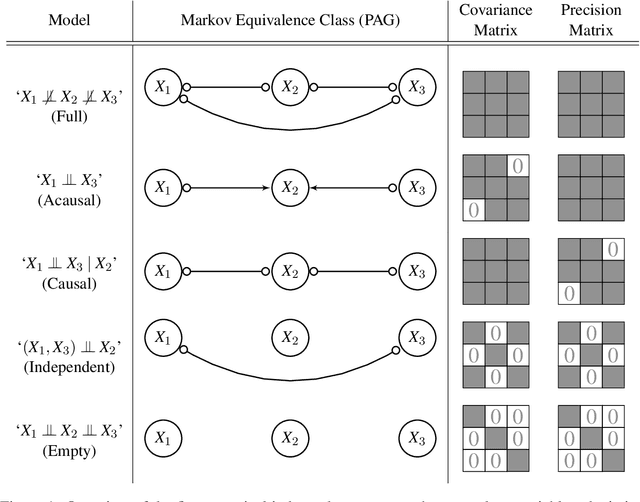
Gene regulatory networks play a crucial role in controlling an organism's biological processes, which is why there is significant interest in developing computational methods that are able to extract their structure from high-throughput genetic data. A typical approach consists of a series of conditional independence tests on the covariance structure meant to progressively reduce the space of possible causal models. We propose a novel efficient Bayesian method for discovering the local causal relationships among triplets of (normally distributed) variables. In our approach, we score the patterns in the covariance matrix in one go and we incorporate the available background knowledge in the form of priors over causal structures. Our method is flexible in the sense that it allows for different types of causal structures and assumptions. We apply the approach to the task of inferring gene regulatory networks by learning regulatory relationships between gene expression levels. We show that our algorithm produces stable and conservative posterior probability estimates over local causal structures that can be used to derive an honest ranking of the most meaningful regulatory relationships. We demonstrate the stability and efficacy of our method both on simulated data and on real-world data from an experiment on yeast.