Optimal Causal Representations and the Causal Information Bottleneck

To effectively study complex causal systems, it is often useful to construct representations that simplify parts of the system by discarding irrelevant details while preserving key features. The Information Bottleneck (IB) method is a widely used approach in representation learning that compresses random variables while retaining information about a target variable. Traditional methods like IB are purely statistical and ignore underlying causal structures, making them ill-suited for causal tasks. We propose the Causal Information Bottleneck (CIB), a causal extension of the IB, which compresses a set of chosen variables while maintaining causal control over a target variable. This method produces representations which are causally interpretable, and which can be used when reasoning about interventions. We present experimental results demonstrating that the learned representations accurately capture causality as intended.

Efficiently Deciding Algebraic Equivalence of Bow-Free Acyclic Path Diagrams

For causal discovery in the presence of latent confounders, constraints beyond conditional independences exist that can enable causal discovery algorithms to distinguish more pairs of graphs. Such constraints are not well-understood yet. In the setting of linear structural equation models without bows, we study algebraic constraints and argue that these provide the most fine-grained resolution achievable. We propose efficient algorithms that decide whether two graphs impose the same algebraic constraints, or whether the constraints imposed by one graph are a subset of those imposed by another graph.

Fundamental Properties of Causal Entropy and Information Gain

Recent developments enable the quantification of causal control given a structural causal model (SCM). This has been accomplished by introducing quantities which encode changes in the entropy of one variable when intervening on another. These measures, named causal entropy and causal information gain, aim to address limitations in existing information theoretical approaches for machine learning tasks where causality plays a crucial role. They have not yet been properly mathematically studied. Our research contributes to the formal understanding of the notions of causal entropy and causal information gain by establishing and analyzing fundamental properties of these concepts, including bounds and chain rules. Furthermore, we elucidate the relationship between causal entropy and stochastic interventions. We also propose definitions for causal conditional entropy and causal conditional information gain. Overall, this exploration paves the way for enhancing causal machine learning tasks through the study of recently-proposed information theoretic quantities grounded in considerations about causality.

Causal Entropy and Information Gain for Measuring Causal Control

Artificial intelligence models and methods commonly lack causal interpretability. Despite the advancements in interpretable machine learning (IML) methods, they frequently assign importance to features which lack causal influence on the outcome variable. Selecting causally relevant features among those identified as relevant by these methods, or even before model training, would offer a solution. Feature selection methods utilizing information theoretical quantities have been successful in identifying statistically relevant features. However, the information theoretical quantities they are based on do not incorporate causality, rendering them unsuitable for such scenarios. To address this challenge, this article proposes information theoretical quantities that incorporate the causal structure of the system, which can be used to evaluate causal importance of features for some given outcome variable. Specifically, we introduce causal versions of entropy and mutual information, termed causal entropy and causal information gain, which are designed to assess how much control a feature provides over the outcome variable. These newly defined quantities capture changes in the entropy of a variable resulting from interventions on other variables. Fundamental results connecting these quantities to the existence of causal effects are derived. The use of causal information gain in feature selection is demonstrated, highlighting its superiority over standard mutual information in revealing which features provide control over a chosen outcome variable. Our investigation paves the way for the development of methods with improved interpretability in domains involving causation.

Graphical Representations for Algebraic Constraints of Linear Structural Equations Models

The observational characteristics of a linear structural equation model can be effectively described by polynomial constraints on the observed covariance matrix. However, these polynomials can be exponentially large, making them impractical for many purposes. In this paper, we present a graphical notation for many of these polynomial constraints. The expressive power of this notation is investigated both theoretically and empirically.

Domain Adaptation by Using Causal Inference to Predict Invariant Conditional Distributions

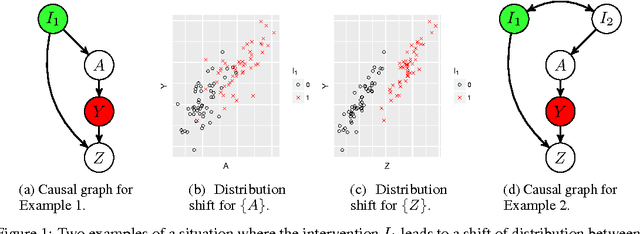
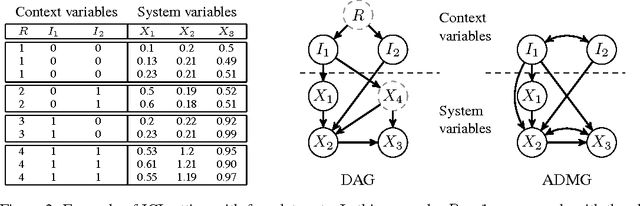
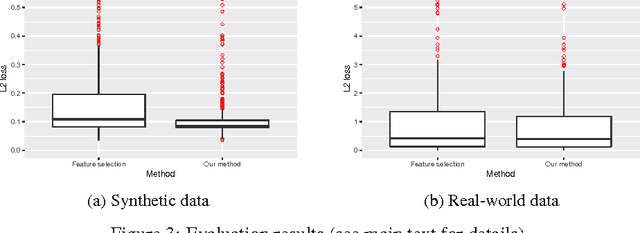
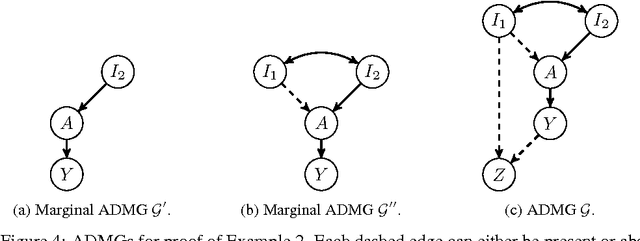
An important goal common to domain adaptation and causal inference is to make accurate predictions when the distributions for the source (or training) domain(s) and target (or test) domain(s) differ. In many cases, these different distributions can be modeled as different contexts of a single underlying system, in which each distribution corresponds to a different perturbation of the system, or in causal terms, an intervention. We focus on a class of such causal domain adaptation problems, where data for one or more source domains are given, and the task is to predict the distribution of a certain target variable from measurements of other variables in one or more target domains. We propose an approach for solving these problems that exploits causal inference and does not rely on prior knowledge of the causal graph, the type of interventions or the intervention targets. We demonstrate our approach by evaluating a possible implementation on simulated and real world data.

Algebraic Equivalence of Linear Structural Equation Models

Despite their popularity, many questions about the algebraic constraints imposed by linear structural equation models remain open problems. For causal discovery, two of these problems are especially important: the enumeration of the constraints imposed by a model, and deciding whether two graphs define the same statistical model. We show how the half-trek criterion can be used to make progress in both of these problems. We apply our theoretical results to a small-scale model selection problem, and find that taking the additional algebraic constraints into account may lead to significant improvements in model selection accuracy.

Combining predictions from linear models when training and test inputs differ

Methods for combining predictions from different models in a supervised learning setting must somehow estimate/predict the quality of a model's predictions at unknown future inputs. Many of these methods (often implicitly) make the assumption that the test inputs are identical to the training inputs, which is seldom reasonable. By failing to take into account that prediction will generally be harder for test inputs that did not occur in the training set, this leads to the selection of too complex models. Based on a novel, unbiased expression for KL divergence, we propose XAIC and its special case FAIC as versions of AIC intended for prediction that use different degrees of knowledge of the test inputs. Both methods substantially differ from and may outperform all the known versions of AIC even when the training and test inputs are iid, and are especially useful for deterministic inputs and under covariate shift. Our experiments on linear models suggest that if the test and training inputs differ substantially, then XAIC and FAIC predictively outperform AIC, BIC and several other methods including Bayesian model averaging.