The Minimal Search Space for Conditional Causal Bandits

Causal knowledge can be used to support decision-making problems. This has been recognized in the causal bandits literature, where a causal (multi-armed) bandit is characterized by a causal graphical model and a target variable. The arms are then interventions on the causal model, and rewards are samples of the target variable. Causal bandits were originally studied with a focus on hard interventions. We focus instead on cases where the arms are conditional interventions, which more accurately model many real-world decision-making problems by allowing the value of the intervened variable to be chosen based on the observed values of other variables. This paper presents a graphical characterization of the minimal set of nodes guaranteed to contain the optimal conditional intervention, which maximizes the expected reward. We then propose an efficient algorithm with a time complexity of $O(|V| + |E|)$ to identify this minimal set of nodes. We prove that the graphical characterization and the proposed algorithm are correct. Finally, we empirically demonstrate that our algorithm significantly prunes the search space and substantially accelerates convergence rates when integrated into standard multi-armed bandit algorithms.

Causal Layering via Conditional Entropy

Causal discovery aims to recover information about an unobserved causal graph from the observable data it generates. Layerings are orderings of the variables which place causes before effects. In this paper, we provide ways to recover layerings of a graph by accessing the data via a conditional entropy oracle, when distributions are discrete. Our algorithms work by repeatedly removing sources or sinks from the graph. Under appropriate assumptions and conditioning, we can separate the sources or sinks from the remainder of the nodes by comparing their conditional entropy to the unconditional entropy of their noise. Our algorithms are provably correct and run in worst-case quadratic time. The main assumptions are faithfulness and injective noise, and either known noise entropies or weakly monotonically increasing noise entropies along directed paths. In addition, we require one of either a very mild extension of faithfulness, or strictly monotonically increasing noise entropies, or expanding noise injectivity to include an additional single argument in the structural functions.

Editing Arbitrary Propositions in LLMs without Subject Labels

Large Language Model (LLM) editing modifies factual information in LLMs. Locate-and-Edit (L\&E) methods accomplish this by finding where relevant information is stored within the neural network, and editing the weights at that location. The goal of editing is to modify the response of an LLM to a proposition independently of its phrasing, while not modifying its response to other related propositions. Existing methods are limited to binary propositions, which represent straightforward binary relations between a subject and an object. Furthermore, existing methods rely on semantic subject labels, which may not be available or even be well-defined in practice. In this paper, we show that both of these issues can be effectively skirted with a simple and fast localization method called Gradient Tracing (GT). This localization method allows editing arbitrary propositions instead of just binary ones, and does so without the need for subject labels. As propositions always have a truth value, our experiments prompt an LLM as a boolean classifier, and edit its T/F response to propositions. Our method applies GT for location tracing, and then edit the model at that location using a mild variant of Rank-One Model Editing (ROME). On datasets of binary propositions derived from the CounterFact dataset, we show that our method -- without access to subject labels -- performs close to state-of-the-art L\&E methods which has access subject labels. We then introduce a new dataset, Factual Accuracy Classification Test (FACT), which includes non-binary propositions and for which subject labels are not generally applicable, and therefore is beyond the scope of existing L\&E methods. Nevertheless, we show that with our method editing is possible on FACT.

On the Unlikelihood of D-Separation

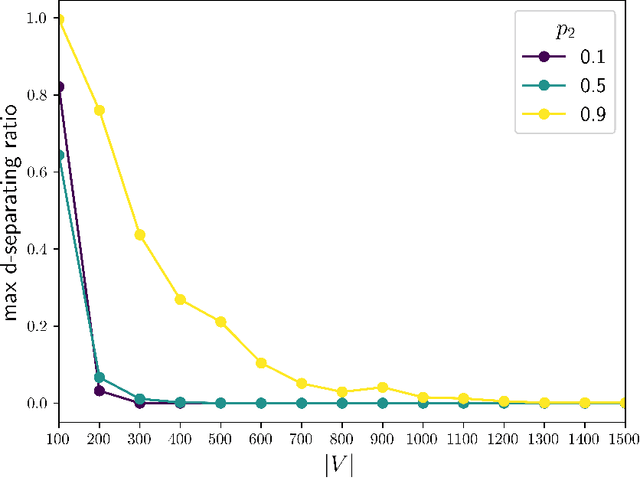
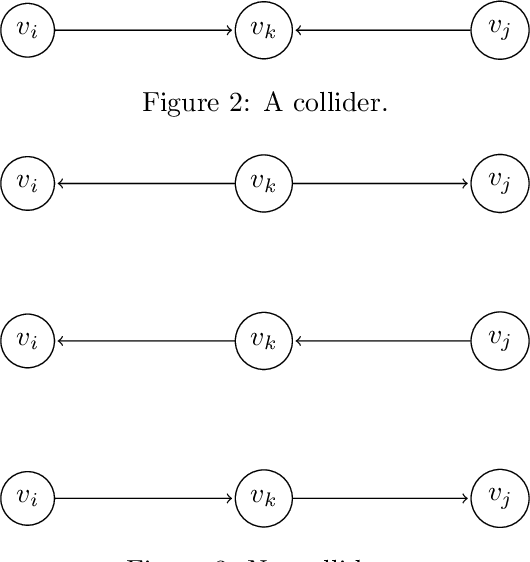
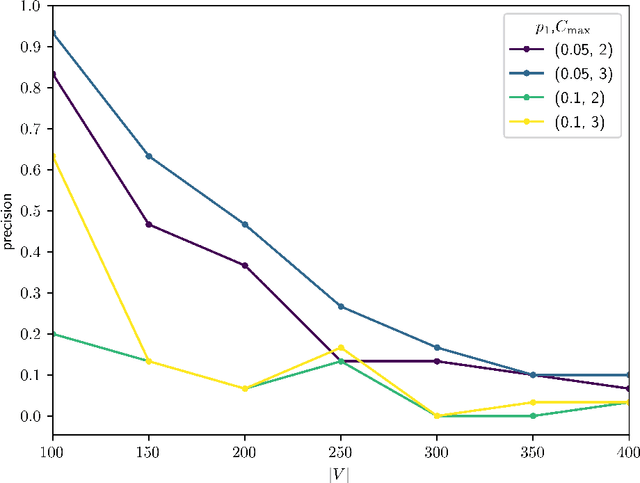
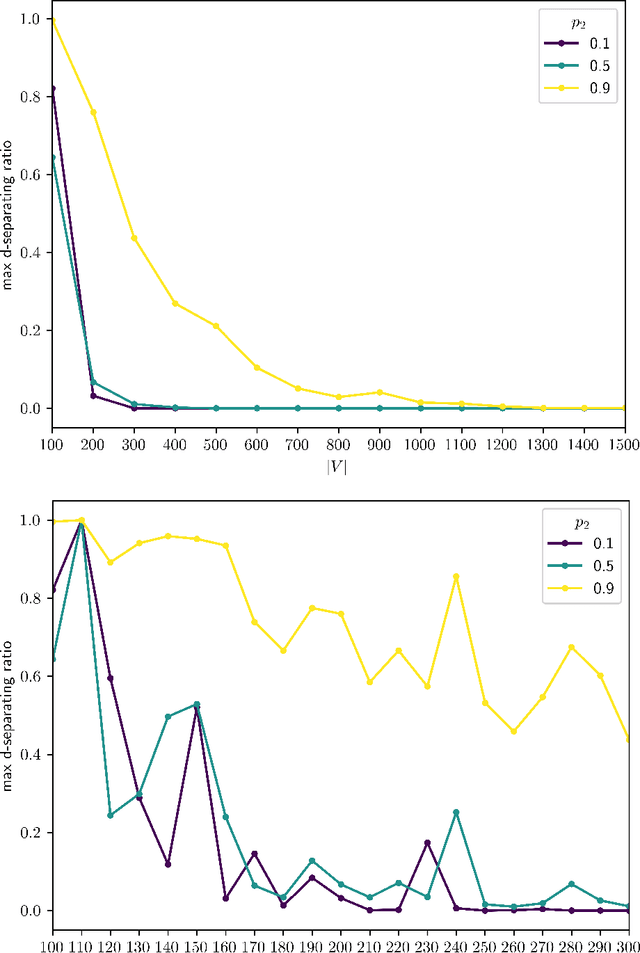
Causal discovery aims to recover a causal graph from data generated by it; constraint based methods do so by searching for a d-separating conditioning set of nodes in the graph via an oracle. In this paper, we provide analytic evidence that on large graphs, d-separation is a rare phenomenon, even when guaranteed to exist, unless the graph is extremely sparse. We then provide an analytic average case analysis of the PC Algorithm for causal discovery, as well as a variant of the SGS Algorithm we call UniformSGS. We consider a set $V=\{v_1,\ldots,v_n\}$ of nodes, and generate a random DAG $G=(V,E)$ where $(v_a, v_b) \in E$ with i.i.d. probability $p_1$ if $a<b$ and $0$ if $a > b$. We provide upper bounds on the probability that a subset of $V-\{x,y\}$ d-separates $x$ and $y$, conditional on $x$ and $y$ being d-separable; our upper bounds decay exponentially fast to $0$ as $|V| \rightarrow \infty$. For the PC Algorithm, while it is known that its worst-case guarantees fail on non-sparse graphs, we show that the same is true for the average case, and that the sparsity requirement is quite demanding: for good performance, the density must go to $0$ as $|V| \rightarrow \infty$ even in the average case. For UniformSGS, while it is known that the running time is exponential for existing edges, we show that in the average case, that is the expected running time for most non-existing edges as well.