Local Constraint-Based Causal Discovery under Selection Bias

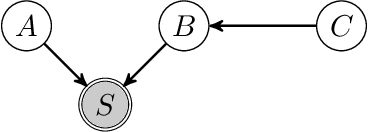
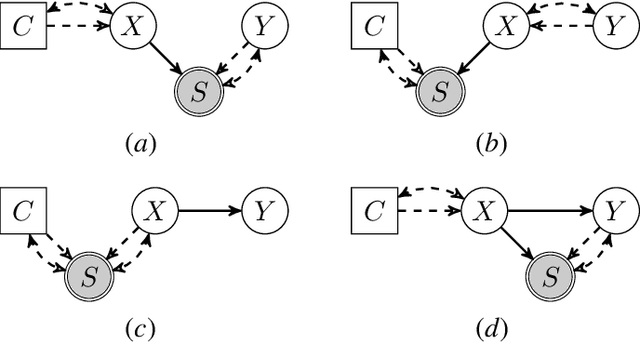
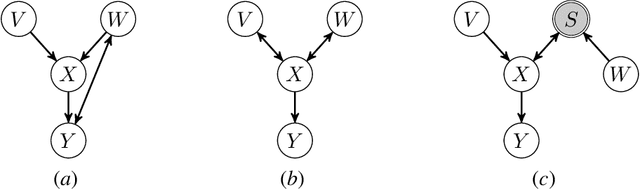
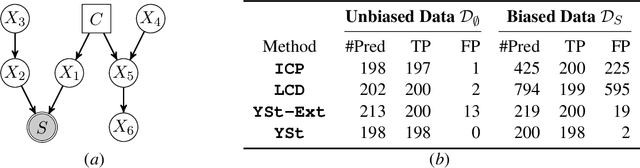
We consider the problem of discovering causal relations from independence constraints selection bias in addition to confounding is present. While the seminal FCI algorithm is sound and complete in this setup, no criterion for the causal interpretation of its output under selection bias is presently known. We focus instead on local patterns of independence relations, where we find no sound method for only three variable that can include background knowledge. Y-Structure patterns are shown to be sound in predicting causal relations from data under selection bias, where cycles may be present. We introduce a finite-sample scoring rule for Y-Structures that is shown to successfully predict causal relations in simulation experiments that include selection mechanisms. On real-world microarray data, we show that a Y-Structure variant performs well across different datasets, potentially circumventing spurious correlations due to selection bias.

Boosting Local Causal Discovery in High-Dimensional Expression Data

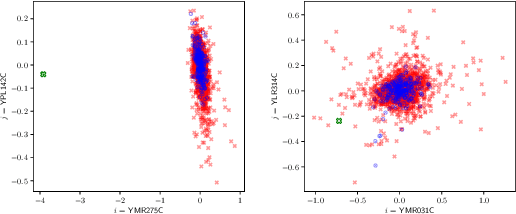
We study the performance of Local Causal Discovery (LCD), a simple and efficient constraint-based method for causal discovery, in predicting causal effects in large-scale gene expression data. We construct practical estimators specific to the high-dimensional regime. Inspired by the ICP algorithm, we use an optional preselection method and two different statistical tests. Empirically, the resulting LCD estimator is seen to closely approach the accuracy of ICP, the state-of-the-art method, while it is algorithmically simpler and computationally more efficient.

Domain Adaptation by Using Causal Inference to Predict Invariant Conditional Distributions

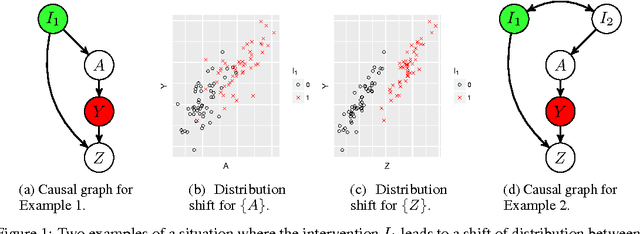
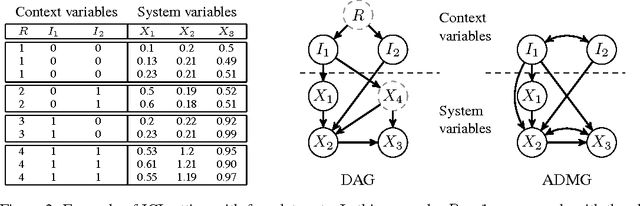
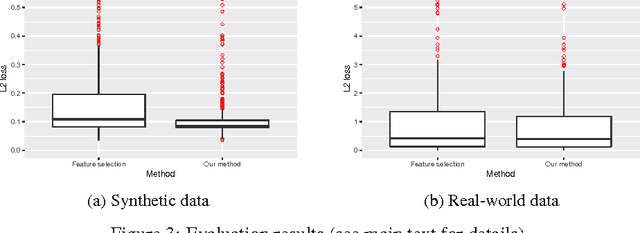
An important goal common to domain adaptation and causal inference is to make accurate predictions when the distributions for the source (or training) domain(s) and target (or test) domain(s) differ. In many cases, these different distributions can be modeled as different contexts of a single underlying system, in which each distribution corresponds to a different perturbation of the system, or in causal terms, an intervention. We focus on a class of such causal domain adaptation problems, where data for one or more source domains are given, and the task is to predict the distribution of a certain target variable from measurements of other variables in one or more target domains. We propose an approach for solving these problems that exploits causal inference and does not rely on prior knowledge of the causal graph, the type of interventions or the intervention targets. We demonstrate our approach by evaluating a possible implementation on simulated and real world data.