Inferring the Direction of a Causal Link and Estimating Its Effect via a Bayesian Mendelian Randomization Approach

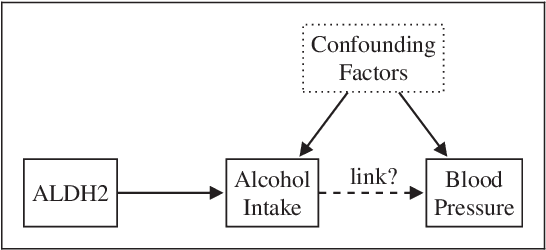
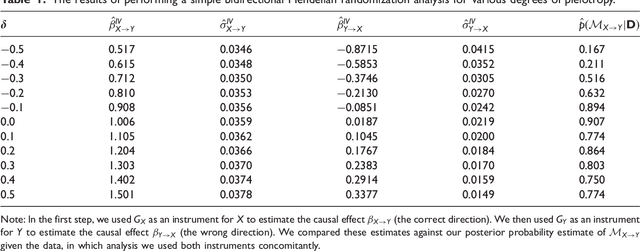
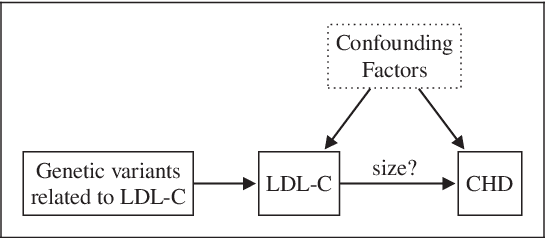
The use of genetic variants as instrumental variables - an approach known as Mendelian randomization - is a popular epidemiological method for estimating the causal effect of an exposure (phenotype, biomarker, risk factor) on a disease or health-related outcome from observational data. Instrumental variables must satisfy strong, often untestable assumptions, which means that finding good genetic instruments among a large list of potential candidates is challenging. This difficulty is compounded by the fact that many genetic variants influence more than one phenotype through different causal pathways, a phenomenon called horizontal pleiotropy. This leads to errors not only in estimating the magnitude of the causal effect but also in inferring the direction of the putative causal link. In this paper, we propose a Bayesian approach called BayesMR that is a generalization of the Mendelian randomization technique in which we allow for pleiotropic effects and, crucially, for the possibility of reverse causation. The output of the method is a posterior distribution over the target causal effect, which provides an immediate and easily interpretable measure of the uncertainty in the estimation. More importantly, we use Bayesian model averaging to determine how much more likely the inferred direction is relative to the reverse direction.

MASSIVE: Tractable and Robust Bayesian Learning of Many-Dimensional Instrumental Variable Models

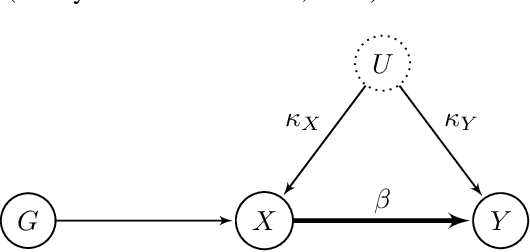
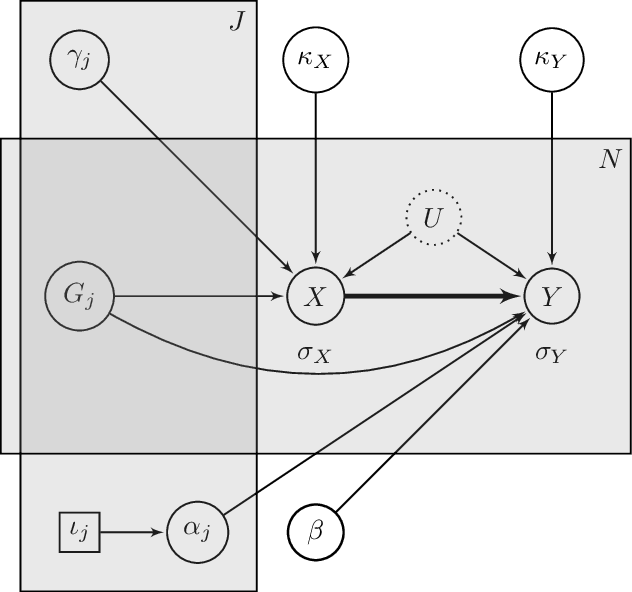
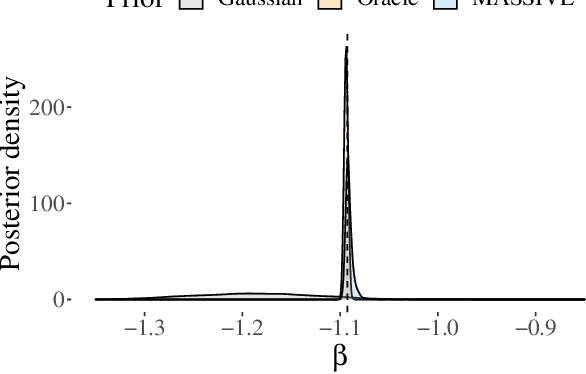
The recent availability of huge, many-dimensional data sets, like those arising from genome-wide association studies (GWAS), provides many opportunities for strengthening causal inference. One popular approach is to utilize these many-dimensional measurements as instrumental variables (instruments) for improving the causal effect estimate between other pairs of variables. Unfortunately, searching for proper instruments in a many-dimensional set of candidates is a daunting task due to the intractable model space and the fact that we cannot directly test which of these candidates are valid, so most existing search methods either rely on overly stringent modeling assumptions or fail to capture the inherent model uncertainty in the selection process. We show that, as long as at least some of the candidates are (close to) valid, without knowing a priori which ones, they collectively still pose enough restrictions on the target interaction to obtain a reliable causal effect estimate. We propose a general and efficient causal inference algorithm that accounts for model uncertainty by performing Bayesian model averaging over the most promising many-dimensional instrumental variable models, while at the same time employing weaker assumptions regarding the data generating process. We showcase the efficiency, robustness and predictive performance of our algorithm through experimental results on both simulated and real-world data.

Causal Shapley Values: Exploiting Causal Knowledge to Explain Individual Predictions of Complex Models

Shapley values underlie one of the most popular model-agnostic methods within explainable artificial intelligence. These values are designed to attribute the difference between a model's prediction and an average baseline to the different features used as input to the model. Being based on solid game-theoretic principles, Shapley values uniquely satisfy several desirable properties, which is why they are increasingly used to explain the predictions of possibly complex and highly non-linear machine learning models. Shapley values are well calibrated to a user's intuition when features are independent, but may lead to undesirable, counterintuitive explanations when the independence assumption is violated. In this paper, we propose a novel framework for computing Shapley values that generalizes recent work that aims to circumvent the independence assumption. By employing Pearl's do-calculus, we show how these 'causal' Shapley values can be derived for general causal graphs without sacrificing any of their desirable properties. Moreover, causal Shapley values enable us to separate the contribution of direct and indirect effects. We provide a practical implementation for computing causal Shapley values based on causal chain graphs when only partial information is available and illustrate their utility on a real-world example.

Large-Scale Local Causal Inference of Gene Regulatory Relationships

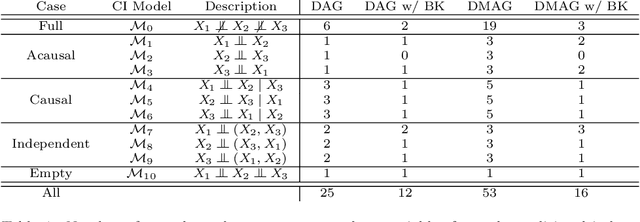
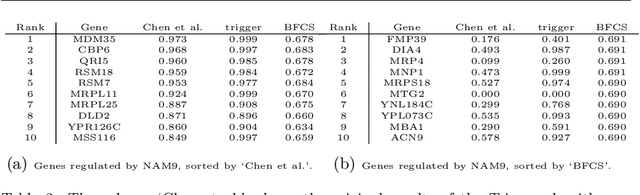
Gene regulatory networks play a crucial role in controlling an organism's biological processes, which is why there is significant interest in developing computational methods that are able to extract their structure from high-throughput genetic data. Many of these computational methods are designed to infer individual regulatory relationships among genes from data on gene expression. We propose a novel efficient Bayesian method for discovering local causal relationships among triplets of (normally distributed) variables. In our approach, we score covariance structures for each triplet in one go and incorporate available background knowledge in the form of priors to derive posterior probabilities over local causal structures. Our method is flexible in the sense that it allows for different types of causal structures and assumptions. We apply our approach to the task of learning causal regulatory relationships among genes. We show that the proposed algorithm produces stable and conservative posterior probability estimates over local causal structures that can be used to derive an honest ranking of the most meaningful regulatory relationships. We demonstrate the stability and efficacy of our method both on simulated data and on real-world data from an experiment on yeast.

A Bayesian Approach for Inferring Local Causal Structure in Gene Regulatory Networks

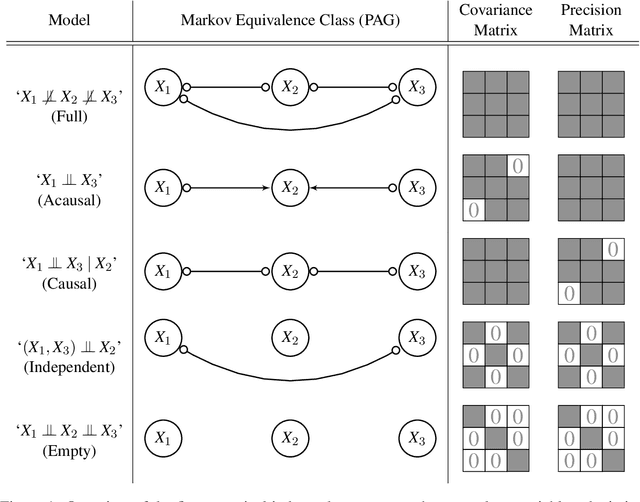
Gene regulatory networks play a crucial role in controlling an organism's biological processes, which is why there is significant interest in developing computational methods that are able to extract their structure from high-throughput genetic data. A typical approach consists of a series of conditional independence tests on the covariance structure meant to progressively reduce the space of possible causal models. We propose a novel efficient Bayesian method for discovering the local causal relationships among triplets of (normally distributed) variables. In our approach, we score the patterns in the covariance matrix in one go and we incorporate the available background knowledge in the form of priors over causal structures. Our method is flexible in the sense that it allows for different types of causal structures and assumptions. We apply the approach to the task of inferring gene regulatory networks by learning regulatory relationships between gene expression levels. We show that our algorithm produces stable and conservative posterior probability estimates over local causal structures that can be used to derive an honest ranking of the most meaningful regulatory relationships. We demonstrate the stability and efficacy of our method both on simulated data and on real-world data from an experiment on yeast.

A Novel Bayesian Approach for Latent Variable Modeling from Mixed Data with Missing Values

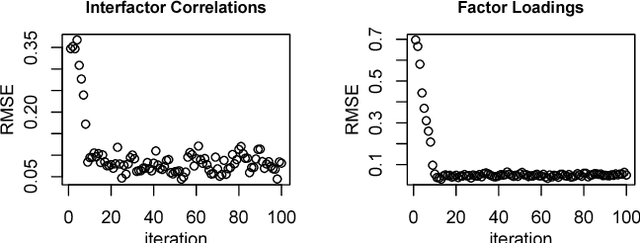
We consider the problem of learning parameters of latent variable models from mixed (continuous and ordinal) data with missing values. We propose a novel Bayesian Gaussian copula factor (BGCF) approach that is consistent under certain conditions and that is quite robust to the violations of these conditions. In simulations, BGCF substantially outperforms two state-of-the-art alternative approaches. An illustration on the `Holzinger & Swineford 1939' dataset indicates that BGCF is favorable over the so-called robust maximum likelihood (MLR) even if the data match the assumptions of MLR.

Robust Causal Estimation in the Large-Sample Limit without Strict Faithfulness

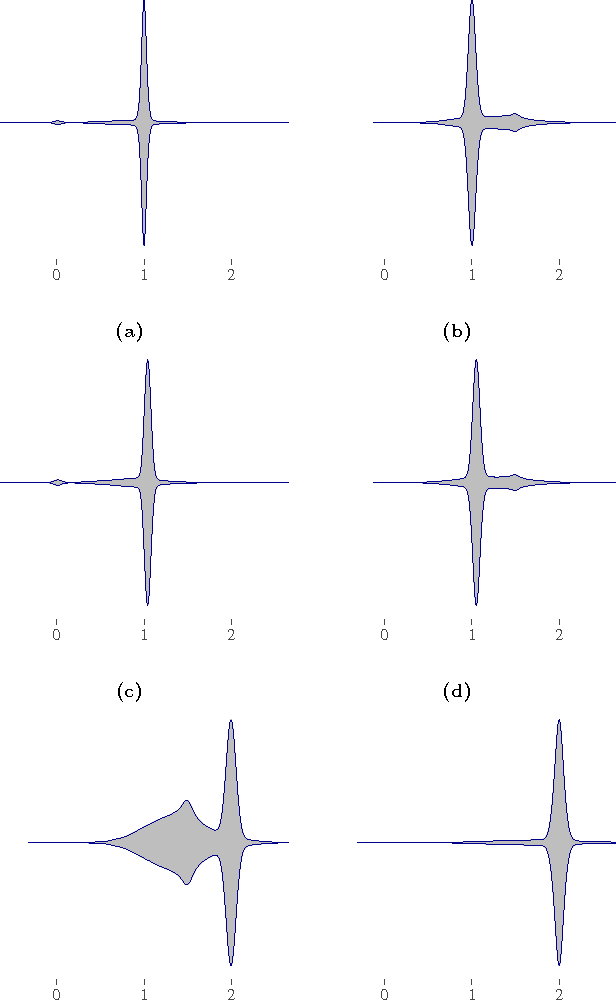
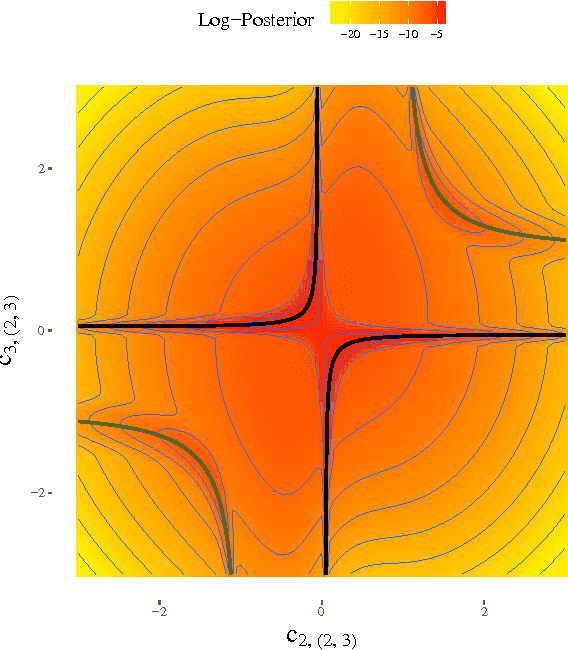
Causal effect estimation from observational data is an important and much studied research topic. The instrumental variable (IV) and local causal discovery (LCD) patterns are canonical examples of settings where a closed-form expression exists for the causal effect of one variable on another, given the presence of a third variable. Both rely on faithfulness to infer that the latter only influences the target effect via the cause variable. In reality, it is likely that this assumption only holds approximately and that there will be at least some form of weak interaction. This brings about the paradoxical situation that, in the large-sample limit, no predictions are made, as detecting the weak edge invalidates the setting. We introduce an alternative approach by replacing strict faithfulness with a prior that reflects the existence of many 'weak' (irrelevant) and 'strong' interactions. We obtain a posterior distribution over the target causal effect estimator which shows that, in many cases, we can still make good estimates. We demonstrate the approach in an application on a simple linear-Gaussian setting, using the MultiNest sampling algorithm, and compare it with established techniques to show our method is robust even when strict faithfulness is violated.