Spectral Mixture Kernels with Time and Phase Delay Dependencies

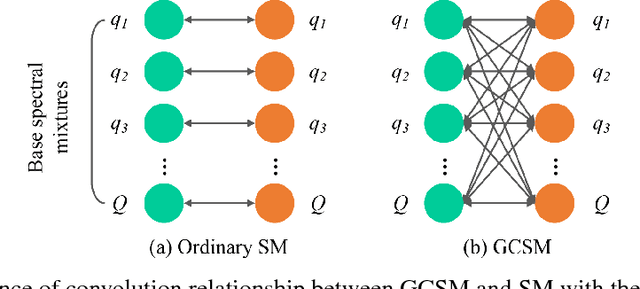
Spectral Mixture (SM) kernels form a powerful class of kernels for Gaussian processes, capable to discover patterns, extrapolate, and model negative co-variances. In SM kernels, spectral mixture components are linearly combined to construct a final flexible kernel. As a consequence SM kernels does not explicitly model correlations between components and dependencies related to time and phase delays between components, because only the auto-convolution of base components are used. To address these drawbacks we introduce Generalized Convolution Spectral Mixture (GCSM) kernels. We incorporate time and phase delay into the base spectral mixture and use cross-convolution between a base component and the complex conjugate of another base component to construct a complex-valued and positive definite kernel representing correlations between base components. In this way the total number of components in GCSM becomes quadratic. We perform a thorough comparative experimental analysis of GCSM on synthetic and real-life datasets. Results indicate the beneficial effect of the extra features of GCSM. This is illustrated in the problem of forecasting the long range trend of a river flow to monitor environment evolution, where GCSM is capable of discovering correlated patterns that SM cannot and improving patterns recognition ability of SM.

Multi-Output Convolution Spectral Mixture for Gaussian Processes

Multi-output Gaussian processes (MOGPs) are recently extended by using spectral mixture kernel, which enables expressively pattern extrapolation with a strong interpretation. In particular, Multi-Output Spectral Mixture kernel (MOSM) is a recent, powerful state of the art method. However, MOSM cannot reduce to the ordinary spectral mixture kernel (SM) when using a single channel. Moreover, when the spectral density of different channels is either very close or very far from each other in the frequency domain, MOSM generates unreasonable scale effects on cross weights which produces an incorrect description of the channel correlation structure. In this paper, we tackle these drawbacks and introduce a principled multi-output convolution spectral mixture kernel (MOCSM) framework. In our framework, we model channel dependencies through convolution of time and phase delayed spectral mixtures between different channels. Results of extensive experiments on synthetic and real datasets demontrate the advantages of MOCSM and its state of the art performance.

Generalized Spectral Mixture Kernels for Multi-Task Gaussian Processes

Multi-Task Gaussian processes (MTGPs) have shown a significant progress both in expressiveness and interpretation of the relatedness between different tasks: from linear combinations of independent single-output Gaussian processes (GPs), through the direct modeling of the cross-covariances such as spectral mixture kernels with phase shift, to the design of multivariate covariance functions based on spectral mixture kernels which model delays among tasks in addition to phase differences, and which provide a parametric interpretation of the relatedness across tasks. In this paper we further extend expressiveness and interpretability of MTGPs models and introduce a new family of kernels capable to model nonlinear correlations between tasks as well as dependencies between spectral mixtures, including time and phase delay. Specifically, we use generalized convolution spectral mixture kernels for modeling dependencies at spectral mixture level, and coupling coregionalization for discovering task level correlations. The proposed kernels for MTGP are validated on artificial data and compared with existing MTGPs methods on three real-world experiments. Results indicate the benefits of our more expressive representation with respect to performance and interpretability.

A Novel Bayesian Approach for Latent Variable Modeling from Mixed Data with Missing Values

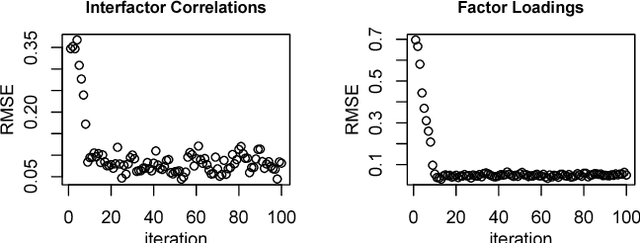
We consider the problem of learning parameters of latent variable models from mixed (continuous and ordinal) data with missing values. We propose a novel Bayesian Gaussian copula factor (BGCF) approach that is consistent under certain conditions and that is quite robust to the violations of these conditions. In simulations, BGCF substantially outperforms two state-of-the-art alternative approaches. An illustration on the `Holzinger & Swineford 1939' dataset indicates that BGCF is favorable over the so-called robust maximum likelihood (MLR) even if the data match the assumptions of MLR.

Stable specification search in structural equation model with latent variables

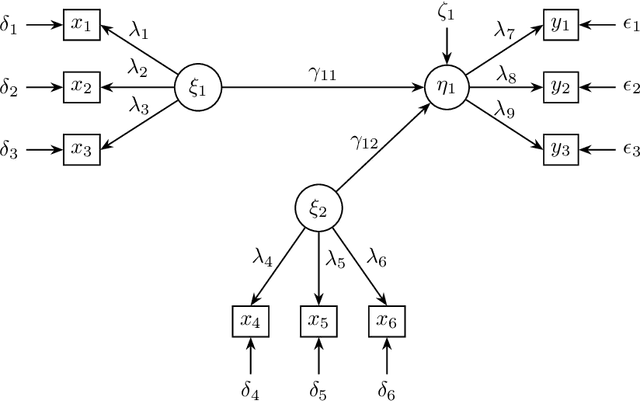
In our previous study, we introduced stable specification search for cross-sectional data (S3C). It is an exploratory causal method that combines stability selection concept and multi-objective optimization to search for stable and parsimonious causal structures across the entire range of model complexities. In this study, we extended S3C to S3C-Latent, to model causal relations between latent variables. We evaluated S3C-Latent on simulated data and compared the results to those of PC-MIMBuild, an extension of the PC algorithm, the state-of-the-art causal discovery method. The comparison showed that S3C-Latent achieved better performance. We also applied S3C-Latent to real-world data of children with attention deficit/hyperactivity disorder and data about measuring mental abilities among pupils. The results are consistent with those of previous studies.

Causality on Longitudinal Data: Stable Specification Search in Constrained Structural Equation Modeling

A typical problem in causal modeling is the instability of model structure learning, i.e., small changes in finite data can result in completely different optimal models. The present work introduces a novel causal modeling algorithm for longitudinal data, that is robust for finite samples based on recent advances in stability selection using subsampling and selection algorithms. Our approach uses exploratory search but allows incorporation of prior knowledge, e.g., the absence of a particular causal relationship between two specific variables. We represent causal relationships using structural equation models. Models are scored along two objectives: the model fit and the model complexity. Since both objectives are often conflicting we apply a multi-objective evolutionary algorithm to search for Pareto optimal models. To handle the instability of small finite data samples, we repeatedly subsample the data and select those substructures (from the optimal models) that are both stable and parsimonious. These substructures can be visualized through a causal graph. Our more exploratory approach achieves at least comparable performance as, but often a significant improvement over state-of-the-art alternative approaches on a simulated data set with a known ground truth. We also present the results of our method on three real-world longitudinal data sets on chronic fatigue syndrome, Alzheimer disease, and chronic kidney disease. The findings obtained with our approach are generally in line with results from more hypothesis-driven analyses in earlier studies and suggest some novel relationships that deserve further research.

Causality on Cross-Sectional Data: Stable Specification Search in Constrained Structural Equation Modeling

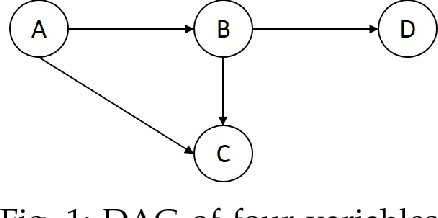
Causal modeling has long been an attractive topic for many researchers and in recent decades there has seen a surge in theoretical development and discovery algorithms. Generally discovery algorithms can be divided into two approaches: constraint-based and score-based. The constraint-based approach is able to detect common causes of the observed variables but the use of independence tests makes it less reliable. The score-based approach produces a result that is easier to interpret as it also measures the reliability of the inferred causal relationships, but it is unable to detect common confounders of the observed variables. A drawback of both score-based and constrained-based approaches is the inherent instability in structure estimation. With finite samples small changes in the data can lead to completely different optimal structures. The present work introduces a new hypothesis-free score-based causal discovery algorithm, called stable specification search, that is robust for finite samples based on recent advances in stability selection using subsampling and selection algorithms. Structure search is performed over Structural Equation Models. Our approach uses exploratory search but allows incorporation of prior background knowledge. We validated our approach on one simulated data set, which we compare to the known ground truth, and two real-world data sets for Chronic Fatigue Syndrome and Attention Deficit Hyperactivity Disorder, which we compare to earlier medical studies. The results on the simulated data set show significant improvement over alternative approaches and the results on the real-word data sets show consistency with the hypothesis driven models constructed by medical experts.