A Novel Bayesian Approach for Latent Variable Modeling from Mixed Data with Missing Values
Paper and Code
Jun 12, 2018

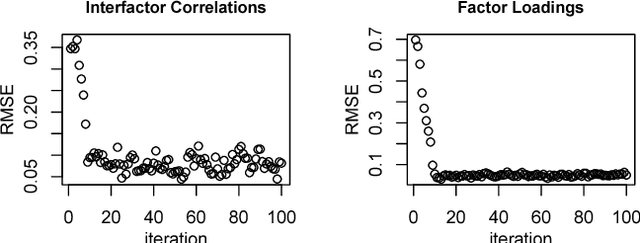

We consider the problem of learning parameters of latent variable models from mixed (continuous and ordinal) data with missing values. We propose a novel Bayesian Gaussian copula factor (BGCF) approach that is consistent under certain conditions and that is quite robust to the violations of these conditions. In simulations, BGCF substantially outperforms two state-of-the-art alternative approaches. An illustration on the `Holzinger & Swineford 1939' dataset indicates that BGCF is favorable over the so-called robust maximum likelihood (MLR) even if the data match the assumptions of MLR.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge