Spectral Mixture Kernels with Time and Phase Delay Dependencies

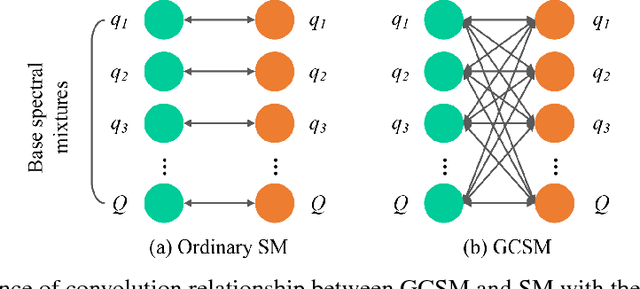
Spectral Mixture (SM) kernels form a powerful class of kernels for Gaussian processes, capable to discover patterns, extrapolate, and model negative co-variances. In SM kernels, spectral mixture components are linearly combined to construct a final flexible kernel. As a consequence SM kernels does not explicitly model correlations between components and dependencies related to time and phase delays between components, because only the auto-convolution of base components are used. To address these drawbacks we introduce Generalized Convolution Spectral Mixture (GCSM) kernels. We incorporate time and phase delay into the base spectral mixture and use cross-convolution between a base component and the complex conjugate of another base component to construct a complex-valued and positive definite kernel representing correlations between base components. In this way the total number of components in GCSM becomes quadratic. We perform a thorough comparative experimental analysis of GCSM on synthetic and real-life datasets. Results indicate the beneficial effect of the extra features of GCSM. This is illustrated in the problem of forecasting the long range trend of a river flow to monitor environment evolution, where GCSM is capable of discovering correlated patterns that SM cannot and improving patterns recognition ability of SM.