Large-Scale Local Causal Inference of Gene Regulatory Relationships
Paper and Code
Sep 10, 2019
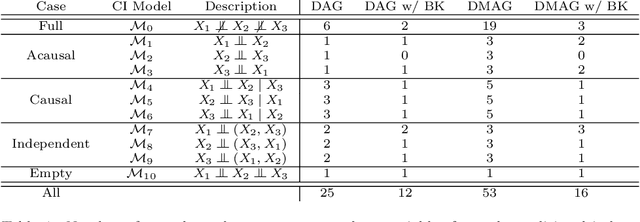

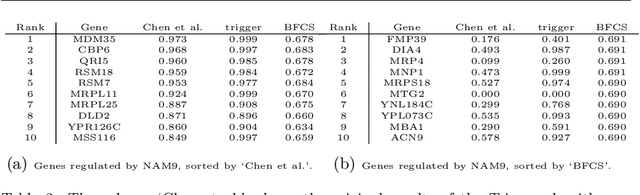
Gene regulatory networks play a crucial role in controlling an organism's biological processes, which is why there is significant interest in developing computational methods that are able to extract their structure from high-throughput genetic data. Many of these computational methods are designed to infer individual regulatory relationships among genes from data on gene expression. We propose a novel efficient Bayesian method for discovering local causal relationships among triplets of (normally distributed) variables. In our approach, we score covariance structures for each triplet in one go and incorporate available background knowledge in the form of priors to derive posterior probabilities over local causal structures. Our method is flexible in the sense that it allows for different types of causal structures and assumptions. We apply our approach to the task of learning causal regulatory relationships among genes. We show that the proposed algorithm produces stable and conservative posterior probability estimates over local causal structures that can be used to derive an honest ranking of the most meaningful regulatory relationships. We demonstrate the stability and efficacy of our method both on simulated data and on real-world data from an experiment on yeast.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge