From MLP to NeoMLP: Leveraging Self-Attention for Neural Fields

Neural fields (NeFs) have recently emerged as a state-of-the-art method for encoding spatio-temporal signals of various modalities. Despite the success of NeFs in reconstructing individual signals, their use as representations in downstream tasks, such as classification or segmentation, is hindered by the complexity of the parameter space and its underlying symmetries, in addition to the lack of powerful and scalable conditioning mechanisms. In this work, we draw inspiration from the principles of connectionism to design a new architecture based on MLPs, which we term NeoMLP. We start from an MLP, viewed as a graph, and transform it from a multi-partite graph to a complete graph of input, hidden, and output nodes, equipped with high-dimensional features. We perform message passing on this graph and employ weight-sharing via self-attention among all the nodes. NeoMLP has a built-in mechanism for conditioning through the hidden and output nodes, which function as a set of latent codes, and as such, NeoMLP can be used straightforwardly as a conditional neural field. We demonstrate the effectiveness of our method by fitting high-resolution signals, including multi-modal audio-visual data. Furthermore, we fit datasets of neural representations, by learning instance-specific sets of latent codes using a single backbone architecture, and then use them for downstream tasks, outperforming recent state-of-the-art methods. The source code is open-sourced at https://github.com/mkofinas/neomlp.

Beyond the Veil of Similarity: Quantifying Semantic Continuity in Explainable AI

We introduce a novel metric for measuring semantic continuity in Explainable AI methods and machine learning models. We posit that for models to be truly interpretable and trustworthy, similar inputs should yield similar explanations, reflecting a consistent semantic understanding. By leveraging XAI techniques, we assess semantic continuity in the task of image recognition. We conduct experiments to observe how incremental changes in input affect the explanations provided by different XAI methods. Through this approach, we aim to evaluate the models' capability to generalize and abstract semantic concepts accurately and to evaluate different XAI methods in correctly capturing the model behaviour. This paper contributes to the broader discourse on AI interpretability by proposing a quantitative measure for semantic continuity for XAI methods, offering insights into the models' and explainers' internal reasoning processes, and promoting more reliable and transparent AI systems.

Amortized Equation Discovery in Hybrid Dynamical Systems

Hybrid dynamical systems are prevalent in science and engineering to express complex systems with continuous and discrete states. To learn the laws of systems, all previous methods for equation discovery in hybrid systems follow a two-stage paradigm, i.e. they first group time series into small cluster fragments and then discover equations in each fragment separately through methods in non-hybrid systems. Although effective, these methods do not fully take advantage of the commonalities in the shared dynamics of multiple fragments that are driven by the same equations. Besides, the two-stage paradigm breaks the interdependence between categorizing and representing dynamics that jointly form hybrid systems. In this paper, we reformulate the problem and propose an end-to-end learning framework, i.e. Amortized Equation Discovery (AMORE), to jointly categorize modes and discover equations characterizing the dynamics of each mode by all segments of the mode. Experiments on four hybrid and six non-hybrid systems show that our method outperforms previous methods on equation discovery, segmentation, and forecasting.

Graph Neural Networks for Learning Equivariant Representations of Neural Networks

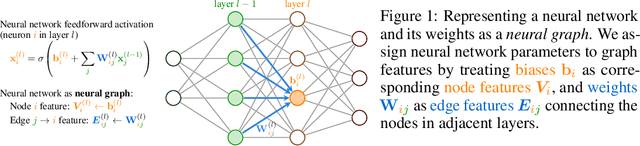
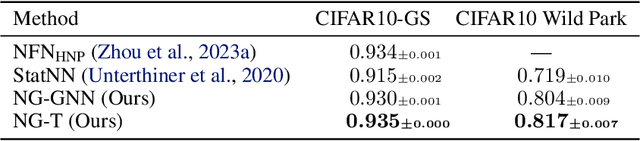
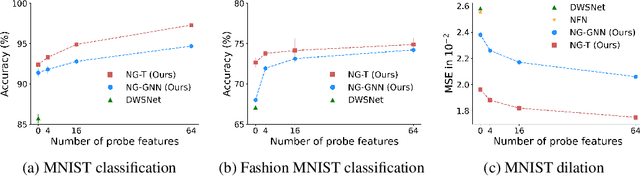
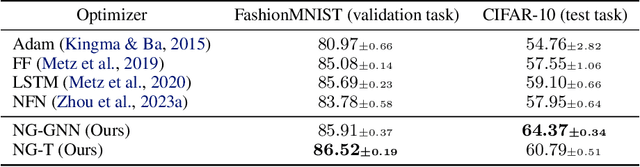
Neural networks that process the parameters of other neural networks find applications in domains as diverse as classifying implicit neural representations, generating neural network weights, and predicting generalization errors. However, existing approaches either overlook the inherent permutation symmetry in the neural network or rely on intricate weight-sharing patterns to achieve equivariance, while ignoring the impact of the network architecture itself. In this work, we propose to represent neural networks as computational graphs of parameters, which allows us to harness powerful graph neural networks and transformers that preserve permutation symmetry. Consequently, our approach enables a single model to encode neural computational graphs with diverse architectures. We showcase the effectiveness of our method on a wide range of tasks, including classification and editing of implicit neural representations, predicting generalization performance, and learning to optimize, while consistently outperforming state-of-the-art methods. The source code is open-sourced at https://github.com/mkofinas/neural-graphs.

How to Train Neural Field Representations: A Comprehensive Study and Benchmark

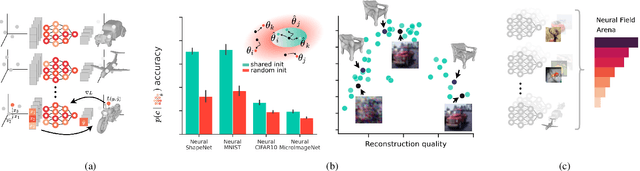
Neural fields (NeFs) have recently emerged as a versatile method for modeling signals of various modalities, including images, shapes, and scenes. Subsequently, a number of works have explored the use of NeFs as representations for downstream tasks, e.g. classifying an image based on the parameters of a NeF that has been fit to it. However, the impact of the NeF hyperparameters on their quality as downstream representation is scarcely understood and remains largely unexplored. This is in part caused by the large amount of time required to fit datasets of neural fields. In this work, we propose $\verb|fit-a-nef|$, a JAX-based library that leverages parallelization to enable fast optimization of large-scale NeF datasets, resulting in a significant speed-up. With this library, we perform a comprehensive study that investigates the effects of different hyperparameters -- including initialization, network architecture, and optimization strategies -- on fitting NeFs for downstream tasks. Our study provides valuable insights on how to train NeFs and offers guidance for optimizing their effectiveness in downstream applications. Finally, based on the proposed library and our analysis, we propose Neural Field Arena, a benchmark consisting of neural field variants of popular vision datasets, including MNIST, CIFAR, variants of ImageNet, and ShapeNetv2. Our library and the Neural Field Arena will be open-sourced to introduce standardized benchmarking and promote further research on neural fields.

Data Augmentations in Deep Weight Spaces

Learning in weight spaces, where neural networks process the weights of other deep neural networks, has emerged as a promising research direction with applications in various fields, from analyzing and editing neural fields and implicit neural representations, to network pruning and quantization. Recent works designed architectures for effective learning in that space, which takes into account its unique, permutation-equivariant, structure. Unfortunately, so far these architectures suffer from severe overfitting and were shown to benefit from large datasets. This poses a significant challenge because generating data for this learning setup is laborious and time-consuming since each data sample is a full set of network weights that has to be trained. In this paper, we address this difficulty by investigating data augmentations for weight spaces, a set of techniques that enable generating new data examples on the fly without having to train additional input weight space elements. We first review several recently proposed data augmentation schemes %that were proposed recently and divide them into categories. We then introduce a novel augmentation scheme based on the Mixup method. We evaluate the performance of these techniques on existing benchmarks as well as new benchmarks we generate, which can be valuable for future studies.

Latent Field Discovery In Interacting Dynamical Systems With Neural Fields

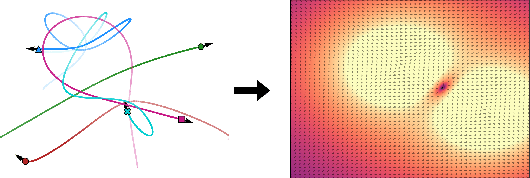
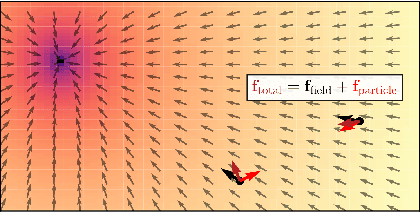
Systems of interacting objects often evolve under the influence of field effects that govern their dynamics, yet previous works have abstracted away from such effects, and assume that systems evolve in a vacuum. In this work, we focus on discovering these fields, and infer them from the observed dynamics alone, without directly observing them. We theorize the presence of latent force fields, and propose neural fields to learn them. Since the observed dynamics constitute the net effect of local object interactions and global field effects, recently popularized equivariant networks are inapplicable, as they fail to capture global information. To address this, we propose to disentangle local object interactions -- which are $\mathrm{SE}(n)$ equivariant and depend on relative states -- from external global field effects -- which depend on absolute states. We model interactions with equivariant graph networks, and combine them with neural fields in a novel graph network that integrates field forces. Our experiments show that we can accurately discover the underlying fields in charged particles settings, traffic scenes, and gravitational n-body problems, and effectively use them to learn the system and forecast future trajectories.

Graph Switching Dynamical Systems

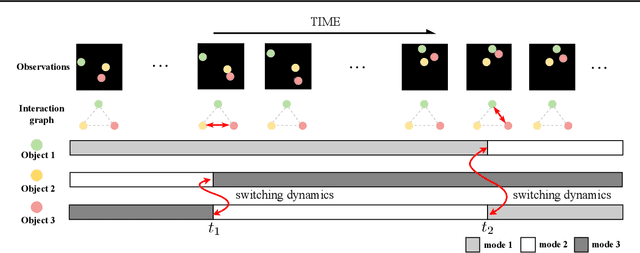
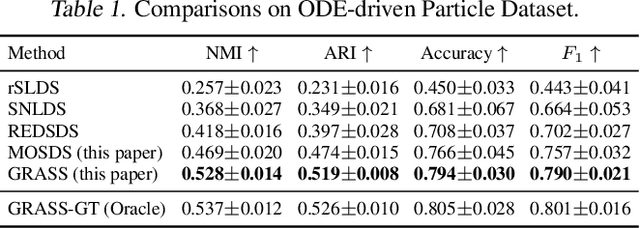
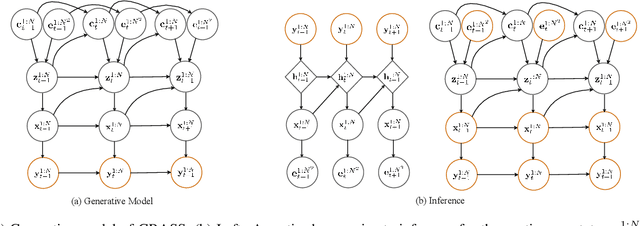
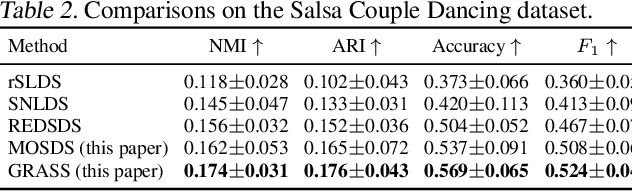
Dynamical systems with complex behaviours, e.g. immune system cells interacting with a pathogen, are commonly modelled by splitting the behaviour into different regimes, or modes, each with simpler dynamics, and then learning the switching behaviour from one mode to another. Switching Dynamical Systems (SDS) are a powerful tool that automatically discovers these modes and mode-switching behaviour from time series data. While effective, these methods focus on independent objects, where the modes of one object are independent of the modes of the other objects. In this paper, we focus on the more general interacting object setting for switching dynamical systems, where the per-object dynamics also depends on an unknown and dynamically changing subset of other objects and their modes. To this end, we propose a novel graph-based approach for switching dynamical systems, GRAph Switching dynamical Systems (GRASS), in which we use a dynamic graph to characterize interactions between objects and learn both intra-object and inter-object mode-switching behaviour. We introduce two new datasets for this setting, a synthesized ODE-driven particles dataset and a real-world Salsa Couple Dancing dataset. Experiments show that GRASS can consistently outperforms previous state-of-the-art methods.

Roto-translated Local Coordinate Frames For Interacting Dynamical Systems

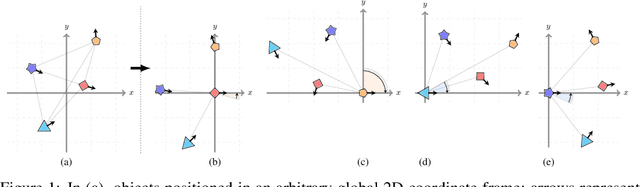
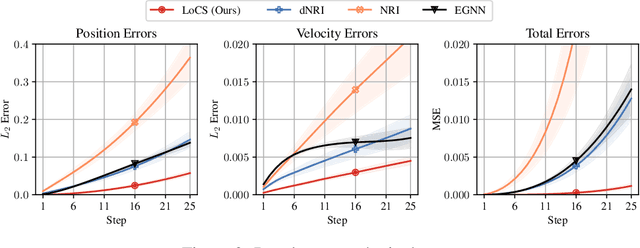
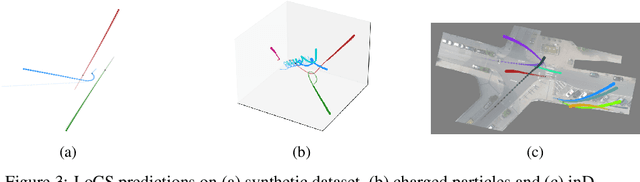
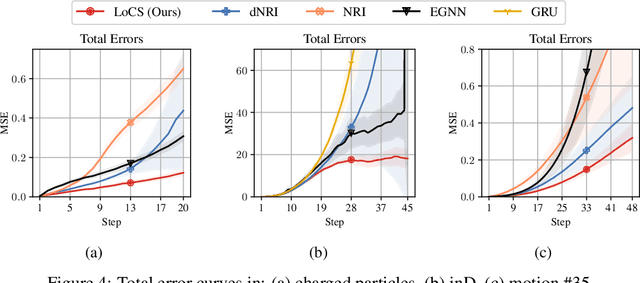
Modelling interactions is critical in learning complex dynamical systems, namely systems of interacting objects with highly non-linear and time-dependent behaviour. A large class of such systems can be formalized as $\textit{geometric graphs}$, $\textit{i.e.}$, graphs with nodes positioned in the Euclidean space given an $\textit{arbitrarily}$ chosen global coordinate system, for instance vehicles in a traffic scene. Notwithstanding the arbitrary global coordinate system, the governing dynamics of the respective dynamical systems are invariant to rotations and translations, also known as $\textit{Galilean invariance}$. As ignoring these invariances leads to worse generalization, in this work we propose local coordinate frames per node-object to induce roto-translation invariance to the geometric graph of the interacting dynamical system. Further, the local coordinate frames allow for a natural definition of anisotropic filtering in graph neural networks. Experiments in traffic scenes, 3D motion capture, and colliding particles demonstrate that the proposed approach comfortably outperforms the recent state-of-the-art.