Ray-Distance Volume Rendering for Neural Scene Reconstruction

Existing methods in neural scene reconstruction utilize the Signed Distance Function (SDF) to model the density function. However, in indoor scenes, the density computed from the SDF for a sampled point may not consistently reflect its real importance in volume rendering, often due to the influence of neighboring objects. To tackle this issue, our work proposes a novel approach for indoor scene reconstruction, which instead parameterizes the density function with the Signed Ray Distance Function (SRDF). Firstly, the SRDF is predicted by the network and transformed to a ray-conditioned density function for volume rendering. We argue that the ray-specific SRDF only considers the surface along the camera ray, from which the derived density function is more consistent to the real occupancy than that from the SDF. Secondly, although SRDF and SDF represent different aspects of scene geometries, their values should share the same sign indicating the underlying spatial occupancy. Therefore, this work introduces a SRDF-SDF consistency loss to constrain the signs of the SRDF and SDF outputs. Thirdly, this work proposes a self-supervised visibility task, introducing the physical visibility geometry to the reconstruction task. The visibility task combines prior from predicted SRDF and SDF as pseudo labels, and contributes to generating more accurate 3D geometry. Our method implemented with different representations has been validated on indoor datasets, achieving improved performance in both reconstruction and view synthesis.

Graph Neural Networks for Learning Equivariant Representations of Neural Networks

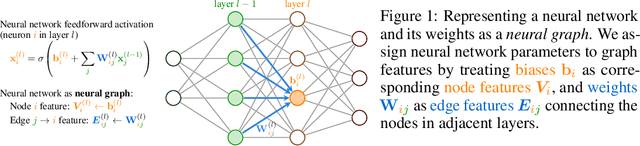
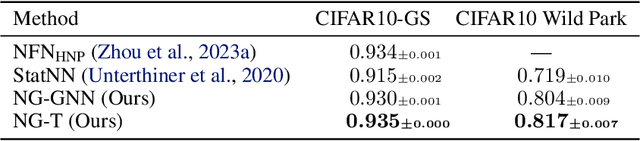
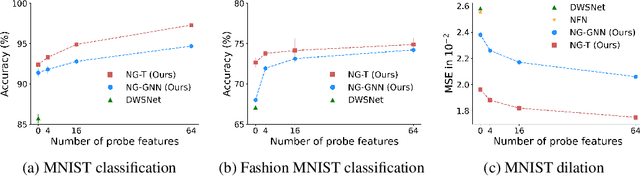
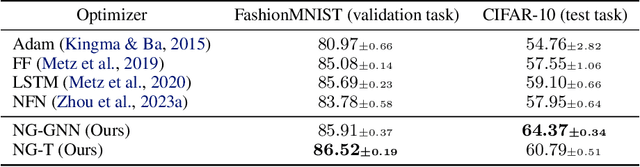
Neural networks that process the parameters of other neural networks find applications in domains as diverse as classifying implicit neural representations, generating neural network weights, and predicting generalization errors. However, existing approaches either overlook the inherent permutation symmetry in the neural network or rely on intricate weight-sharing patterns to achieve equivariance, while ignoring the impact of the network architecture itself. In this work, we propose to represent neural networks as computational graphs of parameters, which allows us to harness powerful graph neural networks and transformers that preserve permutation symmetry. Consequently, our approach enables a single model to encode neural computational graphs with diverse architectures. We showcase the effectiveness of our method on a wide range of tasks, including classification and editing of implicit neural representations, predicting generalization performance, and learning to optimize, while consistently outperforming state-of-the-art methods. The source code is open-sourced at https://github.com/mkofinas/neural-graphs.

Guided Diffusion from Self-Supervised Diffusion Features

Guidance serves as a key concept in diffusion models, yet its effectiveness is often limited by the need for extra data annotation or classifier pretraining. That is why guidance was harnessed from self-supervised learning backbones, like DINO. However, recent studies have revealed that the feature representation derived from diffusion model itself is discriminative for numerous downstream tasks as well, which prompts us to propose a framework to extract guidance from, and specifically for, diffusion models. Our research has yielded several significant contributions. Firstly, the guidance signals from diffusion models are on par with those from class-conditioned diffusion models. Secondly, feature regularization, when based on the Sinkhorn-Knopp algorithm, can further enhance feature discriminability in comparison to unconditional diffusion models. Thirdly, we have constructed an online training approach that can concurrently derive guidance from diffusion models for diffusion models. Lastly, we have extended the application of diffusion models along the constant velocity path of ODE to achieve a more favorable balance between sampling steps and fidelity. The performance of our methods has been outstanding, outperforming related baseline comparisons in large-resolution datasets, such as ImageNet256, ImageNet256-100 and LSUN-Churches. Our code will be released.

Motion Flow Matching for Human Motion Synthesis and Editing

Human motion synthesis is a fundamental task in computer animation. Recent methods based on diffusion models or GPT structure demonstrate commendable performance but exhibit drawbacks in terms of slow sampling speeds and error accumulation. In this paper, we propose \emph{Motion Flow Matching}, a novel generative model designed for human motion generation featuring efficient sampling and effectiveness in motion editing applications. Our method reduces the sampling complexity from thousand steps in previous diffusion models to just ten steps, while achieving comparable performance in text-to-motion and action-to-motion generation benchmarks. Noticeably, our approach establishes a new state-of-the-art Fr\'echet Inception Distance on the KIT-ML dataset. What is more, we tailor a straightforward motion editing paradigm named \emph{sampling trajectory rewriting} leveraging the ODE-style generative models and apply it to various editing scenarios including motion prediction, motion in-between prediction, motion interpolation, and upper-body editing. Our code will be released.

Kernel Learning in Ridge Regression "Automatically" Yields Exact Low Rank Solution

We consider kernels of the form $(x,x') \mapsto \phi(\|x-x'\|^2_\Sigma)$ parametrized by $\Sigma$. For such kernels, we study a variant of the kernel ridge regression problem which simultaneously optimizes the prediction function and the parameter $\Sigma$ of the reproducing kernel Hilbert space. The eigenspace of the $\Sigma$ learned from this kernel ridge regression problem can inform us which directions in covariate space are important for prediction. Assuming that the covariates have nonzero explanatory power for the response only through a low dimensional subspace (central mean subspace), we find that the global minimizer of the finite sample kernel learning objective is also low rank with high probability. More precisely, the rank of the minimizing $\Sigma$ is with high probability bounded by the dimension of the central mean subspace. This phenomenon is interesting because the low rankness property is achieved without using any explicit regularization of $\Sigma$, e.g., nuclear norm penalization. Our theory makes correspondence between the observed phenomenon and the notion of low rank set identifiability from the optimization literature. The low rankness property of the finite sample solutions exists because the population kernel learning objective grows "sharply" when moving away from its minimizers in any direction perpendicular to the central mean subspace.

3D Equivariant Graph Implicit Functions

In recent years, neural implicit representations have made remarkable progress in modeling of 3D shapes with arbitrary topology. In this work, we address two key limitations of such representations, in failing to capture local 3D geometric fine details, and to learn from and generalize to shapes with unseen 3D transformations. To this end, we introduce a novel family of graph implicit functions with equivariant layers that facilitates modeling fine local details and guaranteed robustness to various groups of geometric transformations, through local $k$-NN graph embeddings with sparse point set observations at multiple resolutions. Our method improves over the existing rotation-equivariant implicit function from 0.69 to 0.89 (IoU) on the ShapeNet reconstruction task. We also show that our equivariant implicit function can be extended to other types of similarity transformations and generalizes to unseen translations and scaling.

Unsharp Mask Guided Filtering

The goal of this paper is guided image filtering, which emphasizes the importance of structure transfer during filtering by means of an additional guidance image. Where classical guided filters transfer structures using hand-designed functions, recent guided filters have been considerably advanced through parametric learning of deep networks. The state-of-the-art leverages deep networks to estimate the two core coefficients of the guided filter. In this work, we posit that simultaneously estimating both coefficients is suboptimal, resulting in halo artifacts and structure inconsistencies. Inspired by unsharp masking, a classical technique for edge enhancement that requires only a single coefficient, we propose a new and simplified formulation of the guided filter. Our formulation enjoys a filtering prior from a low-pass filter and enables explicit structure transfer by estimating a single coefficient. Based on our proposed formulation, we introduce a successive guided filtering network, which provides multiple filtering results from a single network, allowing for a trade-off between accuracy and efficiency. Extensive ablations, comparisons and analysis show the effectiveness and efficiency of our formulation and network, resulting in state-of-the-art results across filtering tasks like upsampling, denoising, and cross-modality filtering. Code is available at \url{https://github.com/shizenglin/Unsharp-Mask-Guided-Filtering}.

PointMixup: Augmentation for Point Clouds

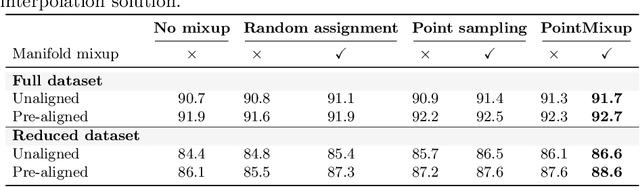
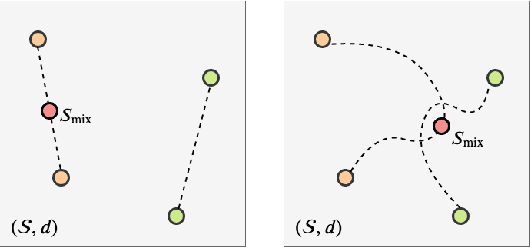
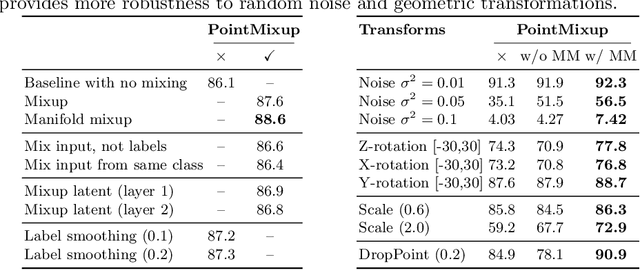
This paper introduces data augmentation for point clouds by interpolation between examples. Data augmentation by interpolation has shown to be a simple and effective approach in the image domain. Such a mixup is however not directly transferable to point clouds, as we do not have a one-to-one correspondence between the points of two different objects. In this paper, we define data augmentation between point clouds as a shortest path linear interpolation. To that end, we introduce PointMixup, an interpolation method that generates new examples through an optimal assignment of the path function between two point clouds. We prove that our PointMixup finds the shortest path between two point clouds and that the interpolation is assignment invariant and linear. With the definition of interpolation, PointMixup allows to introduce strong interpolation-based regularizers such as mixup and manifold mixup to the point cloud domain. Experimentally, we show the potential of PointMixup for point cloud classification, especially when examples are scarce, as well as increased robustness to noise and geometric transformations to points. The code for PointMixup and the experimental details are publicly available.

3D Neighborhood Convolution: Learning Depth-Aware Features for RGB-D and RGB Semantic Segmentation

A key challenge for RGB-D segmentation is how to effectively incorporate 3D geometric information from the depth channel into 2D appearance features. We propose to model the effective receptive field of 2D convolution based on the scale and locality from the 3D neighborhood. Standard convolutions are local in the image space ($u, v$), often with a fixed receptive field of 3x3 pixels. We propose to define convolutions local with respect to the corresponding point in the 3D real-world space ($x, y, z$), where the depth channel is used to adapt the receptive field of the convolution, which yields the resulting filters invariant to scale and focusing on the certain range of depth. We introduce 3D Neighborhood Convolution (3DN-Conv), a convolutional operator around 3D neighborhoods. Further, we can use estimated depth to use our RGB-D based semantic segmentation model from RGB input. Experimental results validate that our proposed 3DN-Conv operator improves semantic segmentation, using either ground-truth depth (RGB-D) or estimated depth (RGB).