RL-finetuning LLMs from on- and off-policy data with a single algorithm

We introduce a novel reinforcement learning algorithm (AGRO, for Any-Generation Reward Optimization) for fine-tuning large-language models. AGRO leverages the concept of generation consistency, which states that the optimal policy satisfies the notion of consistency across any possible generation of the model. We derive algorithms that find optimal solutions via the sample-based policy gradient and provide theoretical guarantees on their convergence. Our experiments demonstrate the effectiveness of AGRO in both on-policy and off-policy settings, showing improved performance on the mathematical reasoning dataset over baseline algorithms.

Soft Policy Optimization: Online Off-Policy RL for Sequence Models

RL-based post-training of language models is almost exclusively done using on-policy methods such as PPO. These methods cannot learn from arbitrary sequences such as those produced earlier in training, in earlier runs, by human experts or other policies, or by decoding and exploration methods. This results in severe sample inefficiency and exploration difficulties, as well as a potential loss of diversity in the policy responses. Moreover, asynchronous PPO implementations require frequent and costly model transfers, and typically use value models which require a large amount of memory. In this paper we introduce Soft Policy Optimization (SPO), a simple, scalable and principled Soft RL method for sequence model policies that can learn from arbitrary online and offline trajectories and does not require a separate value model. In experiments on code contests, we shows that SPO outperforms PPO on pass@10, is significantly faster and more memory efficient, is able to benefit from off-policy data, enjoys improved stability, and learns more diverse (i.e. soft) policies.

Ada-HGNN: Adaptive Sampling for Scalable Hypergraph Neural Networks

Hypergraphs serve as an effective model for depicting complex connections in various real-world scenarios, from social to biological networks. The development of Hypergraph Neural Networks (HGNNs) has emerged as a valuable method to manage the intricate associations in data, though scalability is a notable challenge due to memory limitations. In this study, we introduce a new adaptive sampling strategy specifically designed for hypergraphs, which tackles their unique complexities in an efficient manner. We also present a Random Hyperedge Augmentation (RHA) technique and an additional Multilayer Perceptron (MLP) module to improve the robustness and generalization capabilities of our approach. Thorough experiments with real-world datasets have proven the effectiveness of our method, markedly reducing computational and memory demands while maintaining performance levels akin to conventional HGNNs and other baseline models. This research paves the way for improving both the scalability and efficacy of HGNNs in extensive applications. We will also make our codebase publicly accessible.

Graph Neural Networks for Learning Equivariant Representations of Neural Networks

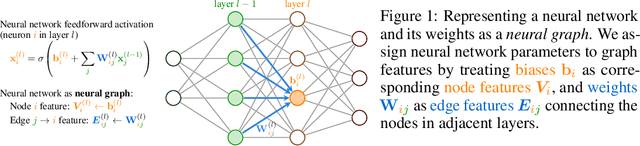
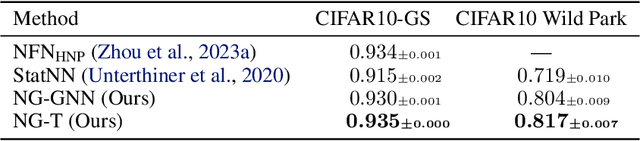
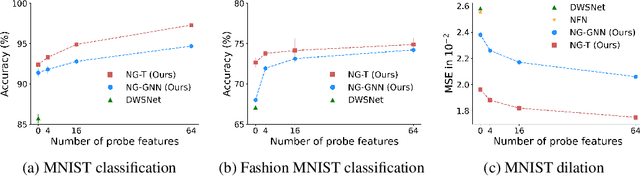
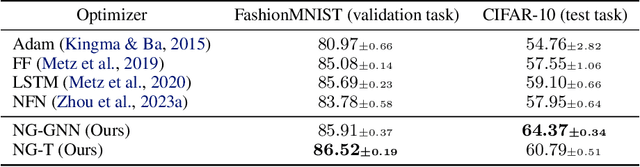
Neural networks that process the parameters of other neural networks find applications in domains as diverse as classifying implicit neural representations, generating neural network weights, and predicting generalization errors. However, existing approaches either overlook the inherent permutation symmetry in the neural network or rely on intricate weight-sharing patterns to achieve equivariance, while ignoring the impact of the network architecture itself. In this work, we propose to represent neural networks as computational graphs of parameters, which allows us to harness powerful graph neural networks and transformers that preserve permutation symmetry. Consequently, our approach enables a single model to encode neural computational graphs with diverse architectures. We showcase the effectiveness of our method on a wide range of tasks, including classification and editing of implicit neural representations, predicting generalization performance, and learning to optimize, while consistently outperforming state-of-the-art methods. The source code is open-sourced at https://github.com/mkofinas/neural-graphs.

Improved Generalization of Weight Space Networks via Augmentations

Learning in deep weight spaces (DWS), where neural networks process the weights of other neural networks, is an emerging research direction, with applications to 2D and 3D neural fields (INRs, NeRFs), as well as making inferences about other types of neural networks. Unfortunately, weight space models tend to suffer from substantial overfitting. We empirically analyze the reasons for this overfitting and find that a key reason is the lack of diversity in DWS datasets. While a given object can be represented by many different weight configurations, typical INR training sets fail to capture variability across INRs that represent the same object. To address this, we explore strategies for data augmentation in weight spaces and propose a MixUp method adapted for weight spaces. We demonstrate the effectiveness of these methods in two setups. In classification, they improve performance similarly to having up to 10 times more data. In self-supervised contrastive learning, they yield substantial 5-10% gains in downstream classification.

Diffusing More Objects for Semi-Supervised Domain Adaptation with Less Labeling

For object detection, it is possible to view the prediction of bounding boxes as a reverse diffusion process. Using a diffusion model, the random bounding boxes are iteratively refined in a denoising step, conditioned on the image. We propose a stochastic accumulator function that starts each run with random bounding boxes and combines the slightly different predictions. We empirically verify that this improves detection performance. The improved detections are leveraged on unlabelled images as weighted pseudo-labels for semi-supervised learning. We evaluate the method on a challenging out-of-domain test set. Our method brings significant improvements and is on par with human-selected pseudo-labels, while not requiring any human involvement.

Data Augmentations in Deep Weight Spaces

Learning in weight spaces, where neural networks process the weights of other deep neural networks, has emerged as a promising research direction with applications in various fields, from analyzing and editing neural fields and implicit neural representations, to network pruning and quantization. Recent works designed architectures for effective learning in that space, which takes into account its unique, permutation-equivariant, structure. Unfortunately, so far these architectures suffer from severe overfitting and were shown to benefit from large datasets. This poses a significant challenge because generating data for this learning setup is laborious and time-consuming since each data sample is a full set of network weights that has to be trained. In this paper, we address this difficulty by investigating data augmentations for weight spaces, a set of techniques that enable generating new data examples on the fly without having to train additional input weight space elements. We first review several recently proposed data augmentation schemes %that were proposed recently and divide them into categories. We then introduce a novel augmentation scheme based on the Mixup method. We evaluate the performance of these techniques on existing benchmarks as well as new benchmarks we generate, which can be valuable for future studies.

Unlocking Slot Attention by Changing Optimal Transport Costs

Slot attention is a powerful method for object-centric modeling in images and videos. However, its set-equivariance limits its ability to handle videos with a dynamic number of objects because it cannot break ties. To overcome this limitation, we first establish a connection between slot attention and optimal transport. Based on this new perspective we propose MESH (Minimize Entropy of Sinkhorn): a cross-attention module that combines the tiebreaking properties of unregularized optimal transport with the speed of regularized optimal transport. We evaluate slot attention using MESH on multiple object-centric learning benchmarks and find significant improvements over slot attention in every setting.

Multiset-Equivariant Set Prediction with Approximate Implicit Differentiation

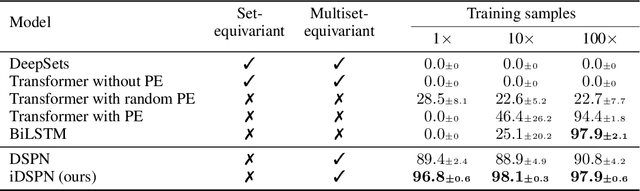
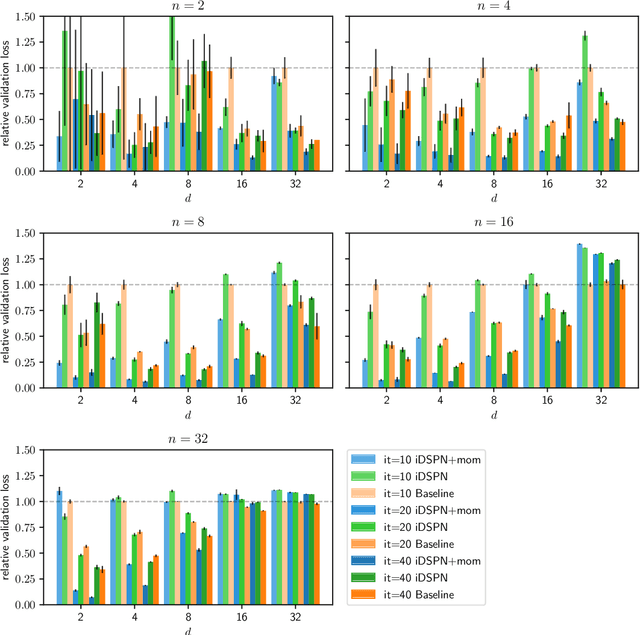
Most set prediction models in deep learning use set-equivariant operations, but they actually operate on multisets. We show that set-equivariant functions cannot represent certain functions on multisets, so we introduce the more appropriate notion of multiset-equivariance. We identify that the existing Deep Set Prediction Network (DSPN) can be multiset-equivariant without being hindered by set-equivariance and improve it with approximate implicit differentiation, allowing for better optimization while being faster and saving memory. In a range of toy experiments, we show that the perspective of multiset-equivariance is beneficial and that our changes to DSPN achieve better results in most cases. On CLEVR object property prediction, we substantially improve over the state-of-the-art Slot Attention from 8% to 77% in one of the strictest evaluation metrics because of the benefits made possible by implicit differentiation.

Recurrently Predicting Hypergraphs

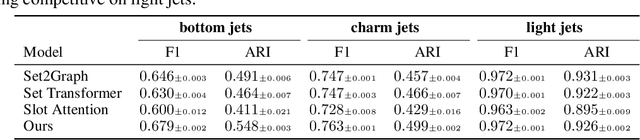
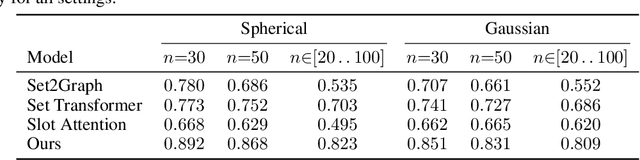
This work considers predicting the relational structure of a hypergraph for a given set of vertices, as common for applications in particle physics, biological systems and other complex combinatorial problems. A problem arises from the number of possible multi-way relationships, or hyperedges, scaling in $\mathcal{O}(2^n)$ for a set of $n$ elements. Simply storing an indicator tensor for all relationships is already intractable for moderately sized $n$, prompting previous approaches to restrict the number of vertices a hyperedge connects. Instead, we propose a recurrent hypergraph neural network that predicts the incidence matrix by iteratively refining an initial guess of the solution. We leverage the property that most hypergraphs of interest are sparsely connected and reduce the memory requirement to $\mathcal{O}(nk)$, where $k$ is the maximum number of positive edges, i.e., edges that actually exist. In order to counteract the linearly growing memory cost from training a lengthening sequence of refinement steps, we further propose an algorithm that applies backpropagation through time on randomly sampled subsequences. We empirically show that our method can match an increase in the intrinsic complexity without a performance decrease and demonstrate superior performance compared to state-of-the-art models.