Recurrently Predicting Hypergraphs

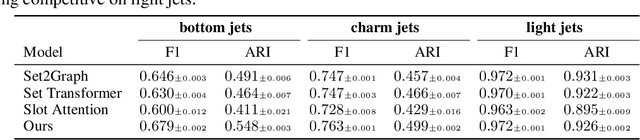
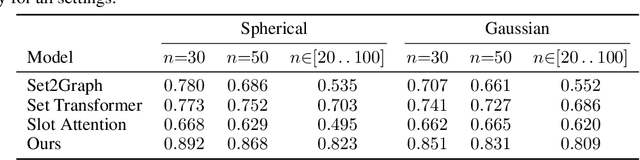
This work considers predicting the relational structure of a hypergraph for a given set of vertices, as common for applications in particle physics, biological systems and other complex combinatorial problems. A problem arises from the number of possible multi-way relationships, or hyperedges, scaling in $\mathcal{O}(2^n)$ for a set of $n$ elements. Simply storing an indicator tensor for all relationships is already intractable for moderately sized $n$, prompting previous approaches to restrict the number of vertices a hyperedge connects. Instead, we propose a recurrent hypergraph neural network that predicts the incidence matrix by iteratively refining an initial guess of the solution. We leverage the property that most hypergraphs of interest are sparsely connected and reduce the memory requirement to $\mathcal{O}(nk)$, where $k$ is the maximum number of positive edges, i.e., edges that actually exist. In order to counteract the linearly growing memory cost from training a lengthening sequence of refinement steps, we further propose an algorithm that applies backpropagation through time on randomly sampled subsequences. We empirically show that our method can match an increase in the intrinsic complexity without a performance decrease and demonstrate superior performance compared to state-of-the-art models.