On the Limitation of Kernel Dependence Maximization for Feature Selection

A simple and intuitive method for feature selection consists of choosing the feature subset that maximizes a nonparametric measure of dependence between the response and the features. A popular proposal from the literature uses the Hilbert-Schmidt Independence Criterion (HSIC) as the nonparametric dependence measure. The rationale behind this approach to feature selection is that important features will exhibit a high dependence with the response and their inclusion in the set of selected features will increase the HSIC. Through counterexamples, we demonstrate that this rationale is flawed and that feature selection via HSIC maximization can miss critical features.

Kernel Learning in Ridge Regression "Automatically" Yields Exact Low Rank Solution

We consider kernels of the form $(x,x') \mapsto \phi(\|x-x'\|^2_\Sigma)$ parametrized by $\Sigma$. For such kernels, we study a variant of the kernel ridge regression problem which simultaneously optimizes the prediction function and the parameter $\Sigma$ of the reproducing kernel Hilbert space. The eigenspace of the $\Sigma$ learned from this kernel ridge regression problem can inform us which directions in covariate space are important for prediction. Assuming that the covariates have nonzero explanatory power for the response only through a low dimensional subspace (central mean subspace), we find that the global minimizer of the finite sample kernel learning objective is also low rank with high probability. More precisely, the rank of the minimizing $\Sigma$ is with high probability bounded by the dimension of the central mean subspace. This phenomenon is interesting because the low rankness property is achieved without using any explicit regularization of $\Sigma$, e.g., nuclear norm penalization. Our theory makes correspondence between the observed phenomenon and the notion of low rank set identifiability from the optimization literature. The low rankness property of the finite sample solutions exists because the population kernel learning objective grows "sharply" when moving away from its minimizers in any direction perpendicular to the central mean subspace.

On the Self-Penalization Phenomenon in Feature Selection

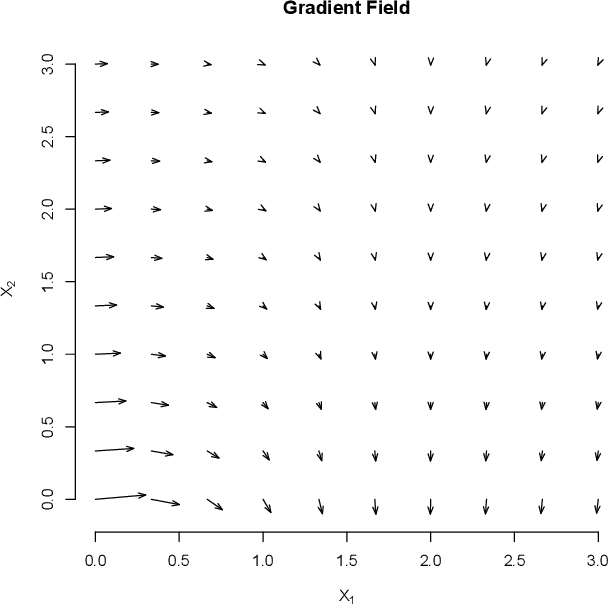
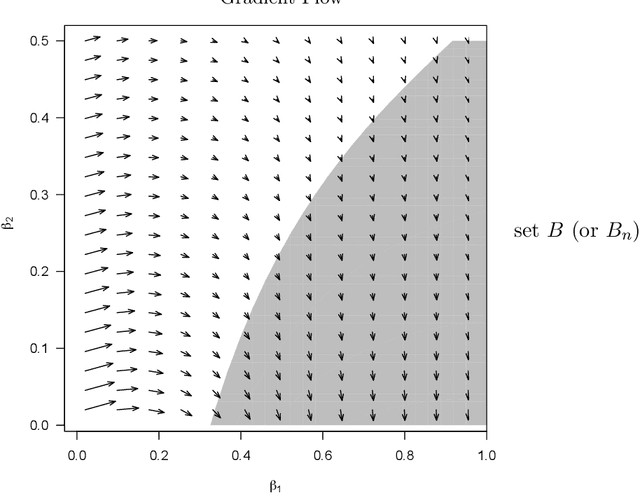
We describe an implicit sparsity-inducing mechanism based on minimization over a family of kernels: \begin{equation*} \min_{\beta, f}~\widehat{\mathbb{E}}[L(Y, f(\beta^{1/q} \odot X)] + \lambda_n \|f\|_{\mathcal{H}_q}^2~~\text{subject to}~~\beta \ge 0, \end{equation*} where $L$ is the loss, $\odot$ is coordinate-wise multiplication and $\mathcal{H}_q$ is the reproducing kernel Hilbert space based on the kernel $k_q(x, x') = h(\|x-x'\|_q^q)$, where $\|\cdot\|_q$ is the $\ell_q$ norm. Using gradient descent to optimize this objective with respect to $\beta$ leads to exactly sparse stationary points with high probability. The sparsity is achieved without using any of the well-known explicit sparsification techniques such as penalization (e.g., $\ell_1$), early stopping or post-processing (e.g., clipping). As an application, we use this sparsity-inducing mechanism to build algorithms consistent for feature selection.

Taming Nonconvexity in Kernel Feature Selection---Favorable Properties of the Laplace Kernel

Kernel-based feature selection is an important tool in nonparametric statistics. Despite many practical applications of kernel-based feature selection, there is little statistical theory available to support the method. A core challenge is the objective function of the optimization problems used to define kernel-based feature selection are nonconvex. The literature has only studied the statistical properties of the \emph{global optima}, which is a mismatch, given that the gradient-based algorithms available for nonconvex optimization are only able to guarantee convergence to local minima. Studying the full landscape associated with kernel-based methods, we show that feature selection objectives using the Laplace kernel (and other $\ell_1$ kernels) come with statistical guarantees that other kernels, including the ubiquitous Gaussian kernel (or other $\ell_2$ kernels) do not possess. Based on a sharp characterization of the gradient of the objective function, we show that $\ell_1$ kernels eliminate unfavorable stationary points that appear when using an $\ell_2$ kernel. Armed with this insight, we establish statistical guarantees for $\ell_1$ kernel-based feature selection which do not require reaching the global minima. In particular, we establish model-selection consistency of $\ell_1$-kernel-based feature selection in recovering main effects and hierarchical interactions in the nonparametric setting with $n \sim \log p$ samples.

A Self-Penalizing Objective Function for Scalable Interaction Detection

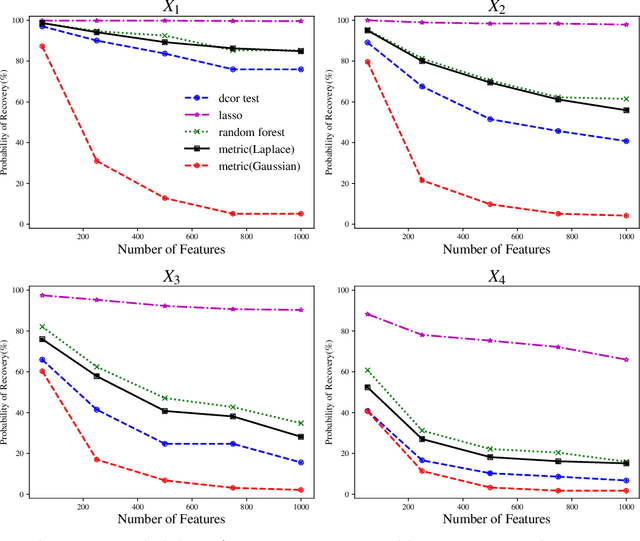
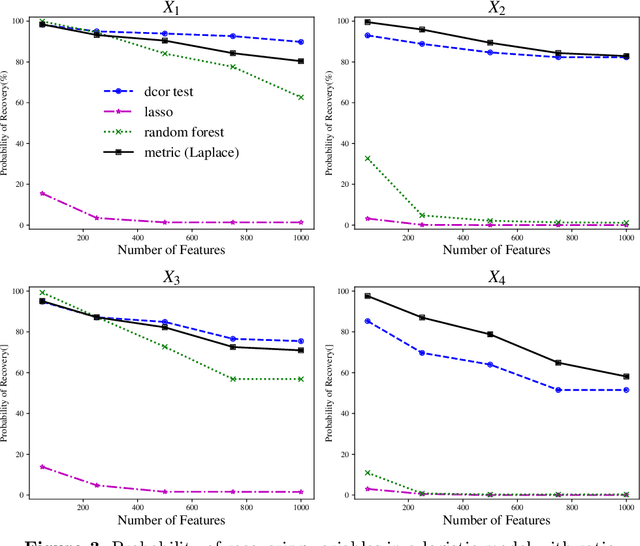
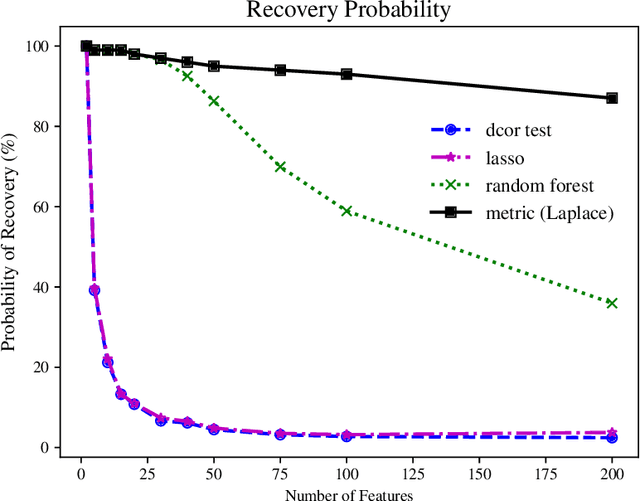
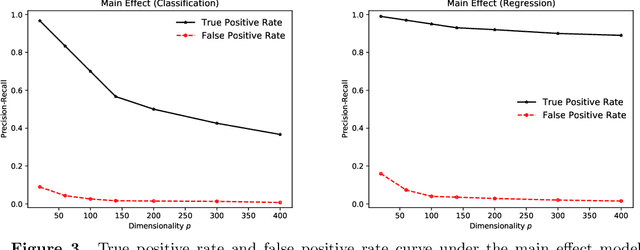
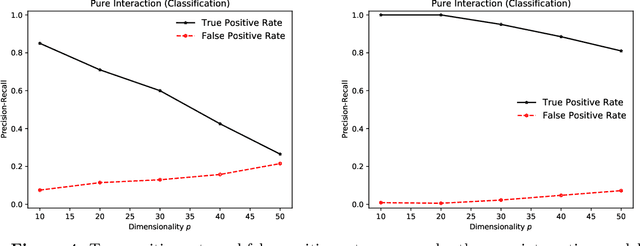
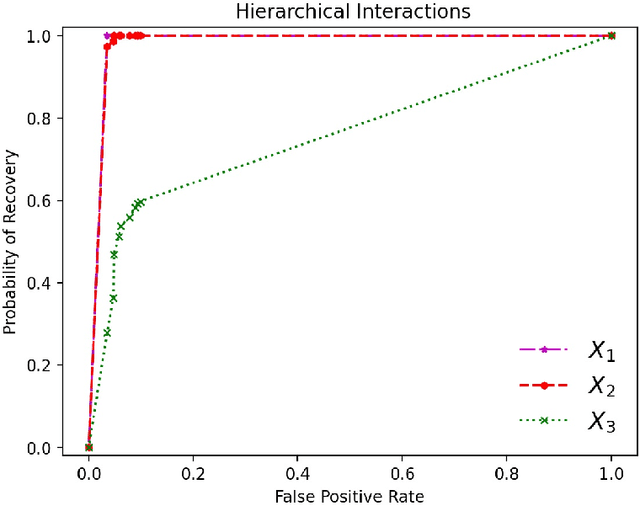
We tackle the problem of nonparametric variable selection with a focus on discovering interactions between variables. With $p$ variables there are $O(p^s)$ possible order-$s$ interactions making exhaustive search infeasible. It is nonetheless possible to identify the variables involved in interactions with only linear computation cost, $O(p)$. The trick is to maximize a class of parametrized nonparametric dependence measures which we call metric learning objectives; the landscape of these nonconvex objective functions is sensitive to interactions but the objectives themselves do not explicitly model interactions. Three properties make metric learning objectives highly attractive: (a) The stationary points of the objective are automatically sparse (i.e. performs selection) -- no explicit $\ell_1$ penalization is needed. (b) All stationary points of the objective exclude noise variables with high probability. (c) Guaranteed recovery of all signal variables without needing to reach the objective's global maxima or special stationary points. The second and third properties mean that all our theoretical results apply in the practical case where one uses gradient ascent to maximize the metric learning objective. While not all metric learning objectives enjoy good statistical power, we design an objective based on $\ell_1$ kernels that does exhibit favorable power: it recovers (i) main effects with $n \sim \log p$ samples, (ii) hierarchical interactions with $n \sim \log p$ samples and (iii) order-$s$ pure interactions with $n \sim p^{2(s-1)}\log p$ samples.