Learning Causal Abstractions of Linear Structural Causal Models
Paper and Code
Jun 01, 2024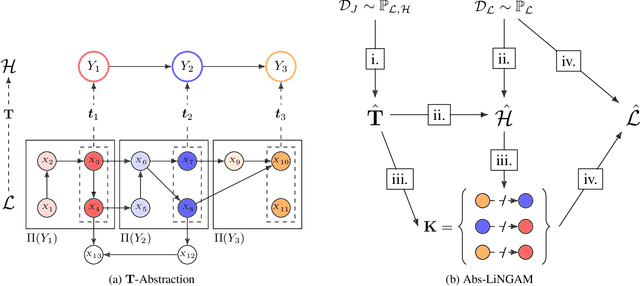
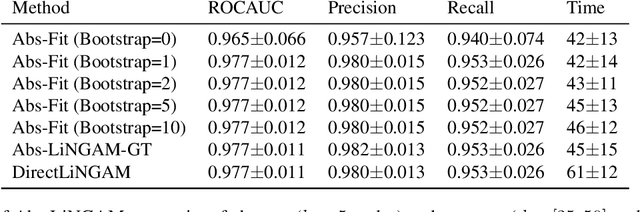
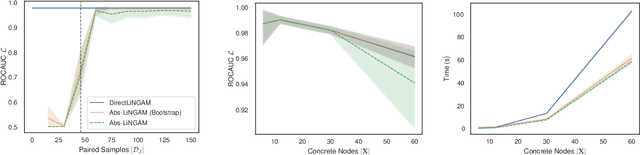
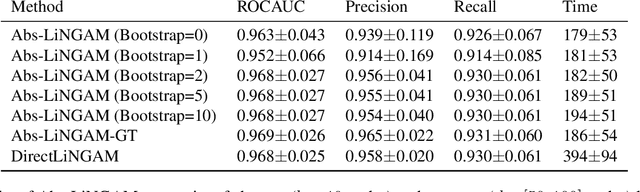
The need for modelling causal knowledge at different levels of granularity arises in several settings. Causal Abstraction provides a framework for formalizing this problem by relating two Structural Causal Models at different levels of detail. Despite increasing interest in applying causal abstraction, e.g. in the interpretability of large machine learning models, the graphical and parametrical conditions under which a causal model can abstract another are not known. Furthermore, learning causal abstractions from data is still an open problem. In this work, we tackle both issues for linear causal models with linear abstraction functions. First, we characterize how the low-level coefficients and the abstraction function determine the high-level coefficients and how the high-level model constrains the causal ordering of low-level variables. Then, we apply our theoretical results to learn high-level and low-level causal models and their abstraction function from observational data. In particular, we introduce Abs-LiNGAM, a method that leverages the constraints induced by the learned high-level model and the abstraction function to speedup the recovery of the larger low-level model, under the assumption of non-Gaussian noise terms. In simulated settings, we show the effectiveness of learning causal abstractions from data and the potential of our method in improving scalability of causal discovery.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge