Near-Optimal Regret for Policy Optimization in Contextual MDPs with General Offline Function Approximation

We introduce \texttt{OPO-CMDP}, the first policy optimization algorithm for stochastic Contextual Markov Decision Process (CMDPs) under general offline function approximation. Our approach achieves a high probability regret bound of $\widetilde{O}(H^4\sqrt{T|S||A|\log(|\mathcal{F}||\mathcal{P}|)}),$ where $S$ and $A$ denote the state and action spaces, $H$ the horizon length, $T$ the number of episodes, and $\mathcal{F}, \mathcal{P}$ the finite function classes used to approximate the losses and dynamics, respectively. This is the first regret bound with optimal dependence on $|S|$ and $|A|$, directly improving the current state-of-the-art (Qian, Hu, and Simchi-Levi, 2024). These results demonstrate that optimistic policy optimization provides a natural, computationally superior and theoretically near-optimal path for solving CMDPs.

Online Weighted Paging with Unknown Weights

Online paging is a fundamental problem in the field of online algorithms, in which one maintains a cache of $k$ slots as requests for fetching pages arrive online. In the weighted variant of this problem, each page has its own fetching cost; a substantial line of work on this problem culminated in an (optimal) $O(\log k)$-competitive randomized algorithm, due to Bansal, Buchbinder and Naor (FOCS'07). Existing work for weighted paging assumes that page weights are known in advance, which is not always the case in practice. For example, in multi-level caching architectures, the expected cost of fetching a memory block is a function of its probability of being in a mid-level cache rather than the main memory. This complex property cannot be predicted in advance; over time, however, one may glean information about page weights through sampling their fetching cost multiple times. We present the first algorithm for online weighted paging that does not know page weights in advance, but rather learns from weight samples. In terms of techniques, this requires providing (integral) samples to a fractional solver, requiring a delicate interface between this solver and the randomized rounding scheme; we believe that our work can inspire online algorithms to other problems that involve cost sampling.

Building Math Agents with Multi-Turn Iterative Preference Learning

Recent studies have shown that large language models' (LLMs) mathematical problem-solving capabilities can be enhanced by integrating external tools, such as code interpreters, and employing multi-turn Chain-of-Thought (CoT) reasoning. While current methods focus on synthetic data generation and Supervised Fine-Tuning (SFT), this paper studies the complementary direct preference learning approach to further improve model performance. However, existing direct preference learning algorithms are originally designed for the single-turn chat task, and do not fully address the complexities of multi-turn reasoning and external tool integration required for tool-integrated mathematical reasoning tasks. To fill in this gap, we introduce a multi-turn direct preference learning framework, tailored for this context, that leverages feedback from code interpreters and optimizes trajectory-level preferences. This framework includes multi-turn DPO and multi-turn KTO as specific implementations. The effectiveness of our framework is validated through training of various language models using an augmented prompt set from the GSM8K and MATH datasets. Our results demonstrate substantial improvements: a supervised fine-tuned Gemma-1.1-it-7B model's performance increased from 77.5% to 83.9% on GSM8K and from 46.1% to 51.2% on MATH. Similarly, a Gemma-2-it-9B model improved from 84.1% to 86.3% on GSM8K and from 51.0% to 54.5% on MATH.

Warm-up Free Policy Optimization: Improved Regret in Linear Markov Decision Processes

Policy Optimization (PO) methods are among the most popular Reinforcement Learning (RL) algorithms in practice. Recently, Sherman et al. [2023a] proposed a PO-based algorithm with rate-optimal regret guarantees under the linear Markov Decision Process (MDP) model. However, their algorithm relies on a costly pure exploration warm-up phase that is hard to implement in practice. This paper eliminates this undesired warm-up phase, replacing it with a simple and efficient contraction mechanism. Our PO algorithm achieves rate-optimal regret with improved dependence on the other parameters of the problem (horizon and function approximation dimension) in two fundamental settings: adversarial losses with full-information feedback and stochastic losses with bandit feedback.

Multi-turn Reinforcement Learning from Preference Human Feedback

Reinforcement Learning from Human Feedback (RLHF) has become the standard approach for aligning Large Language Models (LLMs) with human preferences, allowing LLMs to demonstrate remarkable abilities in various tasks. Existing methods work by emulating the preferences at the single decision (turn) level, limiting their capabilities in settings that require planning or multi-turn interactions to achieve a long-term goal. In this paper, we address this issue by developing novel methods for Reinforcement Learning (RL) from preference feedback between two full multi-turn conversations. In the tabular setting, we present a novel mirror-descent-based policy optimization algorithm for the general multi-turn preference-based RL problem, and prove its convergence to Nash equilibrium. To evaluate performance, we create a new environment, Education Dialogue, where a teacher agent guides a student in learning a random topic, and show that a deep RL variant of our algorithm outperforms RLHF baselines. Finally, we show that in an environment with explicit rewards, our algorithm recovers the same performance as a reward-based RL baseline, despite relying solely on a weaker preference signal.

Near-Optimal Regret in Linear MDPs with Aggregate Bandit Feedback

In many real-world applications, it is hard to provide a reward signal in each step of a Reinforcement Learning (RL) process and more natural to give feedback when an episode ends. To this end, we study the recently proposed model of RL with Aggregate Bandit Feedback (RL-ABF), where the agent only observes the sum of rewards at the end of an episode instead of each reward individually. Prior work studied RL-ABF only in tabular settings, where the number of states is assumed to be small. In this paper, we extend ABF to linear function approximation and develop two efficient algorithms with near-optimal regret guarantees: a value-based optimistic algorithm built on a new randomization technique with a Q-functions ensemble, and a policy optimization algorithm that uses a novel hedging scheme over the ensemble.

A Unified Analysis of Nonstochastic Delayed Feedback for Combinatorial Semi-Bandits, Linear Bandits, and MDPs

We derive a new analysis of Follow The Regularized Leader (FTRL) for online learning with delayed bandit feedback. By separating the cost of delayed feedback from that of bandit feedback, our analysis allows us to obtain new results in three important settings. On the one hand, we derive the first optimal (up to logarithmic factors) regret bounds for combinatorial semi-bandits with delay and adversarial Markov decision processes with delay (and known transition functions). On the other hand, we use our analysis to derive an efficient algorithm for linear bandits with delay achieving near-optimal regret bounds. Our novel regret decomposition shows that FTRL remains stable across multiple rounds under mild assumptions on the Hessian of the regularizer.

Delay-Adapted Policy Optimization and Improved Regret for Adversarial MDP with Delayed Bandit Feedback

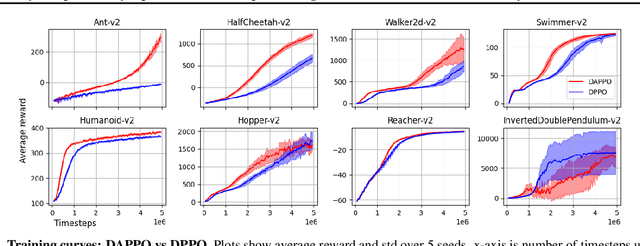
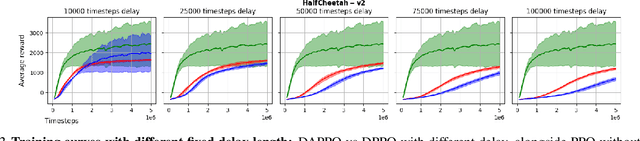
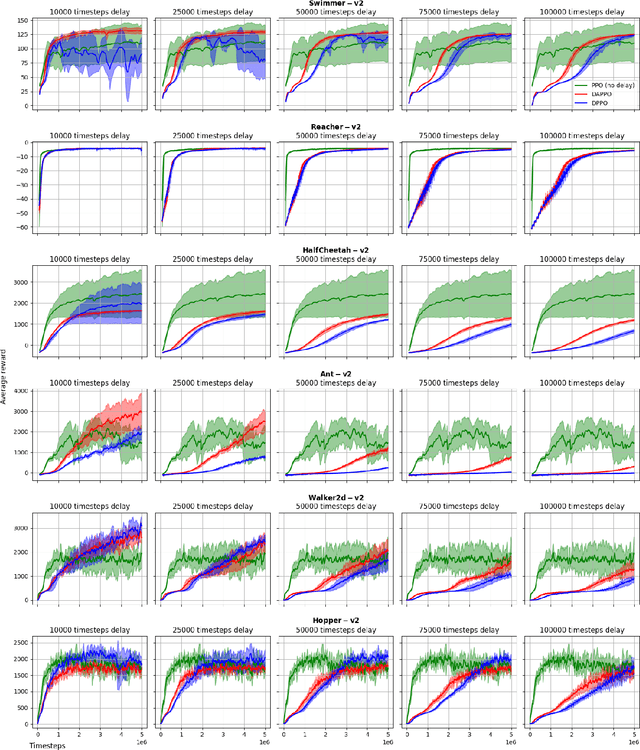
Policy Optimization (PO) is one of the most popular methods in Reinforcement Learning (RL). Thus, theoretical guarantees for PO algorithms have become especially important to the RL community. In this paper, we study PO in adversarial MDPs with a challenge that arises in almost every real-world application -- \textit{delayed bandit feedback}. We give the first near-optimal regret bounds for PO in tabular MDPs, and may even surpass state-of-the-art (which uses less efficient methods). Our novel Delay-Adapted PO (DAPO) is easy to implement and to generalize, allowing us to extend our algorithm to: (i) infinite state space under the assumption of linear $Q$-function, proving the first regret bounds for delayed feedback with function approximation. (ii) deep RL, demonstrating its effectiveness in experiments on MuJoCo domains.

Policy Optimization for Stochastic Shortest Path

Policy optimization is among the most popular and successful reinforcement learning algorithms, and there is increasing interest in understanding its theoretical guarantees. In this work, we initiate the study of policy optimization for the stochastic shortest path (SSP) problem, a goal-oriented reinforcement learning model that strictly generalizes the finite-horizon model and better captures many applications. We consider a wide range of settings, including stochastic and adversarial environments under full information or bandit feedback, and propose a policy optimization algorithm for each setting that makes use of novel correction terms and/or variants of dilated bonuses (Luo et al., 2021). For most settings, our algorithm is shown to achieve a near-optimal regret bound. One key technical contribution of this work is a new approximation scheme to tackle SSP problems that we call \textit{stacked discounted approximation} and use in all our proposed algorithms. Unlike the finite-horizon approximation that is heavily used in recent SSP algorithms, our new approximation enables us to learn a near-stationary policy with only logarithmic changes during an episode and could lead to an exponential improvement in space complexity.

Near-Optimal Regret for Adversarial MDP with Delayed Bandit Feedback

The standard assumption in reinforcement learning (RL) is that agents observe feedback for their actions immediately. However, in practice feedback is often observed in delay. This paper studies online learning in episodic Markov decision process (MDP) with unknown transitions, adversarially changing costs, and unrestricted delayed bandit feedback. More precisely, the feedback for the agent in episode $k$ is revealed only in the end of episode $k + d^k$, where the delay $d^k$ can be changing over episodes and chosen by an oblivious adversary. We present the first algorithms that achieve near-optimal $\sqrt{K + D}$ regret, where $K$ is the number of episodes and $D = \sum_{k=1}^K d^k$ is the total delay, significantly improving upon the best known regret bound of $(K + D)^{2/3}$.