No-Regret Online Reinforcement Learning with Adversarial Losses and Transitions

Existing online learning algorithms for adversarial Markov Decision Processes achieve ${O}(\sqrt{T})$ regret after $T$ rounds of interactions even if the loss functions are chosen arbitrarily by an adversary, with the caveat that the transition function has to be fixed. This is because it has been shown that adversarial transition functions make no-regret learning impossible. Despite such impossibility results, in this work, we develop algorithms that can handle both adversarial losses and adversarial transitions, with regret increasing smoothly in the degree of maliciousness of the adversary. More concretely, we first propose an algorithm that enjoys $\widetilde{{O}}(\sqrt{T} + C^{\textsf{P}})$ regret where $C^{\textsf{P}}$ measures how adversarial the transition functions are and can be at most ${O}(T)$. While this algorithm itself requires knowledge of $C^{\textsf{P}}$, we further develop a black-box reduction approach that removes this requirement. Moreover, we also show that further refinements of the algorithm not only maintains the same regret bound, but also simultaneously adapts to easier environments (where losses are generated in a certain stochastically constrained manner as in Jin et al. [2021]) and achieves $\widetilde{{O}}(U + \sqrt{UC^{\textsf{L}}} + C^{\textsf{P}})$ regret, where $U$ is some standard gap-dependent coefficient and $C^{\textsf{L}}$ is the amount of corruption on losses.

Heterogeneous Directed Hypergraph Neural Network over abstract syntax tree (AST) for Code Classification

Code classification is a difficult issue in program understanding and automatic coding. Due to the elusive syntax and complicated semantics in programs, most existing studies use techniques based on abstract syntax tree (AST) and graph neural network (GNN) to create code representations for code classification. These techniques utilize the structure and semantic information of the code, but they only take into account pairwise associations and neglect the high-order correlations that already exist between nodes in the AST, which may result in the loss of code structural information. On the other hand, while a general hypergraph can encode high-order data correlations, it is homogeneous and undirected which will result in a lack of semantic and structural information such as node types, edge types, and directions between child nodes and parent nodes when modeling AST. In this study, we propose to represent AST as a heterogeneous directed hypergraph (HDHG) and process the graph by heterogeneous directed hypergraph neural network (HDHGN) for code classification. Our method improves code understanding and can represent high-order data correlations beyond paired interactions. We assess heterogeneous directed hypergraph neural network (HDHGN) on public datasets of Python and Java programs. Our method outperforms previous AST-based and GNN-based methods, which demonstrates the capability of our model.

Improved Best-of-Both-Worlds Guarantees for Multi-Armed Bandits: FTRL with General Regularizers and Multiple Optimal Arms

We study the problem of designing adaptive multi-armed bandit algorithms that perform optimally in both the stochastic setting and the adversarial setting simultaneously (often known as a best-of-both-world guarantee). A line of recent works shows that when configured and analyzed properly, the Follow-the-Regularized-Leader (FTRL) algorithm, originally designed for the adversarial setting, can in fact optimally adapt to the stochastic setting as well. Such results, however, critically rely on an assumption that there exists one unique optimal arm. Recently, Ito (2021) took the first step to remove such an undesirable uniqueness assumption for one particular FTRL algorithm with the $\frac{1}{2}$-Tsallis entropy regularizer. In this work, we significantly improve and generalize this result, showing that uniqueness is unnecessary for FTRL with a broad family of regularizers and a new learning rate schedule. For some regularizers, our regret bounds also improve upon prior results even when uniqueness holds. We further provide an application of our results to the decoupled exploration and exploitation problem, demonstrating that our techniques are broadly applicable.

Near-Optimal Regret for Adversarial MDP with Delayed Bandit Feedback

The standard assumption in reinforcement learning (RL) is that agents observe feedback for their actions immediately. However, in practice feedback is often observed in delay. This paper studies online learning in episodic Markov decision process (MDP) with unknown transitions, adversarially changing costs, and unrestricted delayed bandit feedback. More precisely, the feedback for the agent in episode $k$ is revealed only in the end of episode $k + d^k$, where the delay $d^k$ can be changing over episodes and chosen by an oblivious adversary. We present the first algorithms that achieve near-optimal $\sqrt{K + D}$ regret, where $K$ is the number of episodes and $D = \sum_{k=1}^K d^k$ is the total delay, significantly improving upon the best known regret bound of $(K + D)^{2/3}$.

The best of both worlds: stochastic and adversarial episodic MDPs with unknown transition

We consider the best-of-both-worlds problem for learning an episodic Markov Decision Process through $T$ episodes, with the goal of achieving $\widetilde{\mathcal{O}}(\sqrt{T})$ regret when the losses are adversarial and simultaneously $\mathcal{O}(\text{polylog}(T))$ regret when the losses are (almost) stochastic. Recent work by [Jin and Luo, 2020] achieves this goal when the fixed transition is known, and leaves the case of unknown transition as a major open question. In this work, we resolve this open problem by using the same Follow-the-Regularized-Leader ($\text{FTRL}$) framework together with a set of new techniques. Specifically, we first propose a loss-shifting trick in the $\text{FTRL}$ analysis, which greatly simplifies the approach of [Jin and Luo, 2020] and already improves their results for the known transition case. Then, we extend this idea to the unknown transition case and develop a novel analysis which upper bounds the transition estimation error by (a fraction of) the regret itself in the stochastic setting, a key property to ensure $\mathcal{O}(\text{polylog}(T))$ regret.

Simultaneously Learning Stochastic and Adversarial Episodic MDPs with Known Transition

This work studies the problem of learning episodic Markov Decision Processes with known transition and bandit feedback. We develop the first algorithm with a ``best-of-both-worlds'' guarantee: it achieves $\mathcal{O}(log T)$ regret when the losses are stochastic, and simultaneously enjoys worst-case robustness with $\tilde{\mathcal{O}}(\sqrt{T})$ regret even when the losses are adversarial, where $T$ is the number of episodes. More generally, it achieves $\tilde{\mathcal{O}}(\sqrt{C})$ regret in an intermediate setting where the losses are corrupted by a total amount of $C$. Our algorithm is based on the Follow-the-Regularized-Leader method from Zimin and Neu (2013), with a novel hybrid regularizer inspired by recent works of Zimmert et al. (2019a, 2019b) for the special case of multi-armed bandits. Crucially, our regularizer admits a non-diagonal Hessian with a highly complicated inverse. Analyzing such a regularizer and deriving a particular self-bounding regret guarantee is our key technical contribution and might be of independent interest.

Learning Adversarial MDPs with Bandit Feedback and Unknown Transition

We consider the problem of learning in episodic finite-horizon Markov decision processes with an unknown transition function, bandit feedback, and adversarial losses. We propose an efficient algorithm that achieves $\mathcal{\tilde{O}}(L|X|\sqrt{|A|T})$ regret with high probability, where $L$ is the horizon, $|X|$ is the number of states, $|A|$ is the number of actions, and $T$ is the number of episodes. To the best of our knowledge, our algorithm is the first to ensure $\mathcal{\tilde{O}}(\sqrt{T})$ regret in this challenging setting; in fact it achieves the same regret bound as (Rosenberg & Mansour, 2019a) that considers an easier setting with full-information feedback. Our key technical contributions are two-fold: a tighter confidence set for the transition function, and an optimistic loss estimator that is inversely weighted by an $\textit{upper occupancy bound}$.

Deep Reinforcement Learning for Multi-Driver Vehicle Dispatching and Repositioning Problem

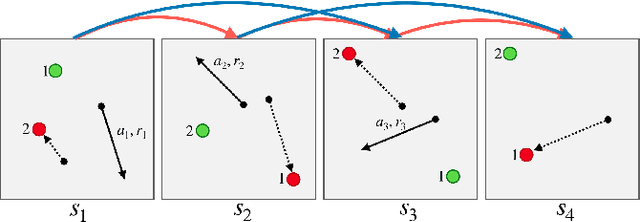
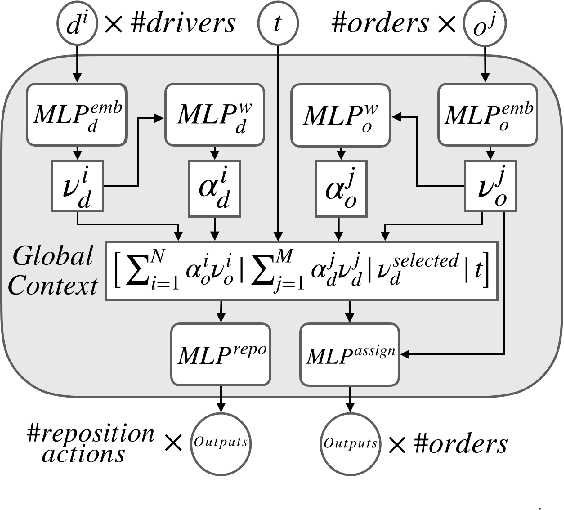
Order dispatching and driver repositioning (also known as fleet management) in the face of spatially and temporally varying supply and demand are central to a ride-sharing platform marketplace. Hand-crafting heuristic solutions that account for the dynamics in these resource allocation problems is difficult, and may be better handled by an end-to-end machine learning method. Previous works have explored machine learning methods to the problem from a high-level perspective, where the learning method is responsible for either repositioning the drivers or dispatching orders, and as a further simplification, the drivers are considered independent agents maximizing their own reward functions. In this paper we present a deep reinforcement learning approach for tackling the full fleet management and dispatching problems. In addition to treating the drivers as individual agents, we consider the problem from a system-centric perspective, where a central fleet management agent is responsible for decision-making for all drivers.