Near-Optimal Regret in Linear MDPs with Aggregate Bandit Feedback

In many real-world applications, it is hard to provide a reward signal in each step of a Reinforcement Learning (RL) process and more natural to give feedback when an episode ends. To this end, we study the recently proposed model of RL with Aggregate Bandit Feedback (RL-ABF), where the agent only observes the sum of rewards at the end of an episode instead of each reward individually. Prior work studied RL-ABF only in tabular settings, where the number of states is assumed to be small. In this paper, we extend ABF to linear function approximation and develop two efficient algorithms with near-optimal regret guarantees: a value-based optimistic algorithm built on a new randomization technique with a Q-functions ensemble, and a policy optimization algorithm that uses a novel hedging scheme over the ensemble.

Delay-Adapted Policy Optimization and Improved Regret for Adversarial MDP with Delayed Bandit Feedback

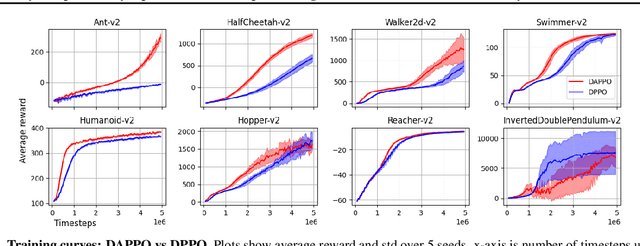
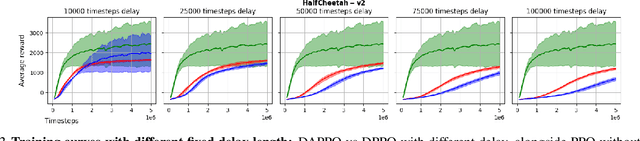
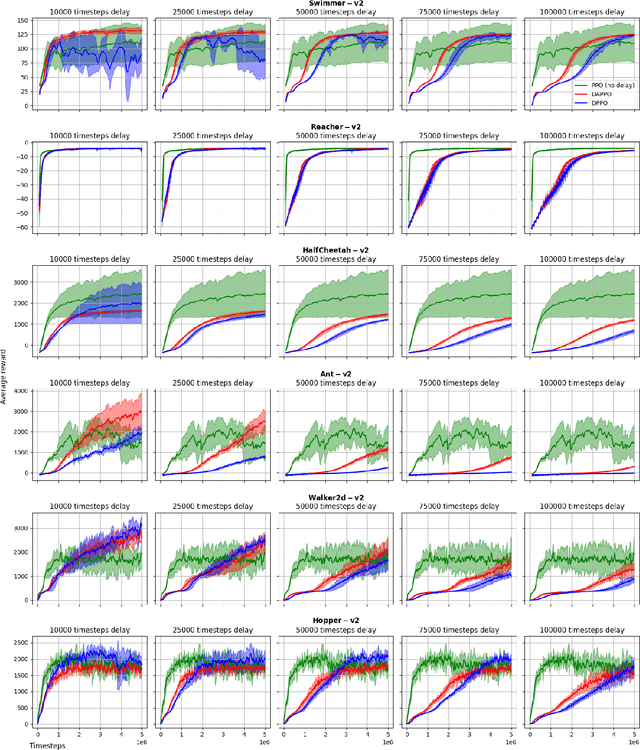
Policy Optimization (PO) is one of the most popular methods in Reinforcement Learning (RL). Thus, theoretical guarantees for PO algorithms have become especially important to the RL community. In this paper, we study PO in adversarial MDPs with a challenge that arises in almost every real-world application -- \textit{delayed bandit feedback}. We give the first near-optimal regret bounds for PO in tabular MDPs, and may even surpass state-of-the-art (which uses less efficient methods). Our novel Delay-Adapted PO (DAPO) is easy to implement and to generalize, allowing us to extend our algorithm to: (i) infinite state space under the assumption of linear $Q$-function, proving the first regret bounds for delayed feedback with function approximation. (ii) deep RL, demonstrating its effectiveness in experiments on MuJoCo domains.