Online Weighted Paging with Unknown Weights

Online paging is a fundamental problem in the field of online algorithms, in which one maintains a cache of $k$ slots as requests for fetching pages arrive online. In the weighted variant of this problem, each page has its own fetching cost; a substantial line of work on this problem culminated in an (optimal) $O(\log k)$-competitive randomized algorithm, due to Bansal, Buchbinder and Naor (FOCS'07). Existing work for weighted paging assumes that page weights are known in advance, which is not always the case in practice. For example, in multi-level caching architectures, the expected cost of fetching a memory block is a function of its probability of being in a mid-level cache rather than the main memory. This complex property cannot be predicted in advance; over time, however, one may glean information about page weights through sampling their fetching cost multiple times. We present the first algorithm for online weighted paging that does not know page weights in advance, but rather learns from weight samples. In terms of techniques, this requires providing (integral) samples to a fractional solver, requiring a delicate interface between this solver and the randomized rounding scheme; we believe that our work can inspire online algorithms to other problems that involve cost sampling.

Batch Ensemble for Variance Dependent Regret in Stochastic Bandits

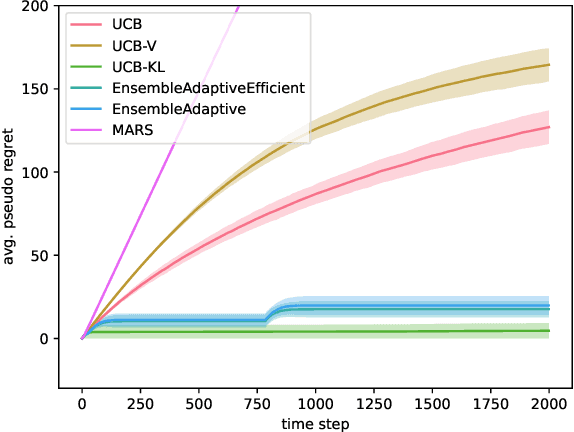
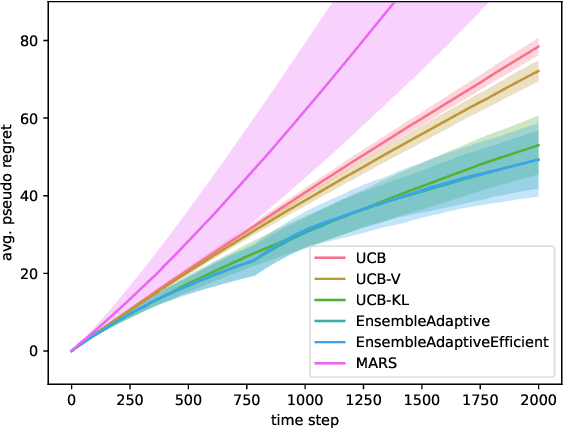
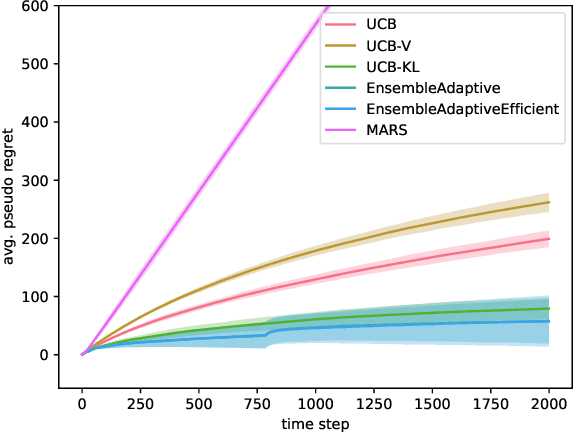
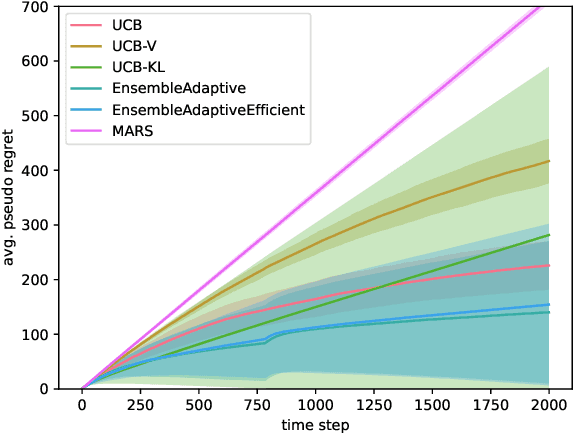
Efficiently trading off exploration and exploitation is one of the key challenges in online Reinforcement Learning (RL). Most works achieve this by carefully estimating the model uncertainty and following the so-called optimistic model. Inspired by practical ensemble methods, in this work we propose a simple and novel batch ensemble scheme that provably achieves near-optimal regret for stochastic Multi-Armed Bandits (MAB). Crucially, our algorithm has just a single parameter, namely the number of batches, and its value does not depend on distributional properties such as the scale and variance of the losses. We complement our theoretical results by demonstrating the effectiveness of our algorithm on synthetic benchmarks.

Efficient Rate Optimal Regret for Adversarial Contextual MDPs Using Online Function Approximation

We present the OMG-CMDP! algorithm for regret minimization in adversarial Contextual MDPs. The algorithm operates under the minimal assumptions of realizable function class and access to online least squares and log loss regression oracles. Our algorithm is efficient (assuming efficient online regression oracles), simple and robust to approximation errors. It enjoys an $\widetilde{O}(H^{2.5} \sqrt{ T|S||A| ( \mathcal{R}(\mathcal{O}) + H \log(\delta^{-1}) )})$ regret guarantee, with $T$ being the number of episodes, $S$ the state space, $A$ the action space, $H$ the horizon and $\mathcal{R}(\mathcal{O}) = \mathcal{R}(\mathcal{O}_{\mathrm{sq}}^\mathcal{F}) + \mathcal{R}(\mathcal{O}_{\mathrm{log}}^\mathcal{P})$ is the sum of the regression oracles' regret, used to approximate the context-dependent rewards and dynamics, respectively. To the best of our knowledge, our algorithm is the first efficient rate optimal regret minimization algorithm for adversarial CMDPs that operates under the minimal standard assumption of online function approximation.

Counterfactual Optimism: Rate Optimal Regret for Stochastic Contextual MDPs

We present the UC$^3$RL algorithm for regret minimization in Stochastic Contextual MDPs (CMDPs). The algorithm operates under the minimal assumptions of realizable function class, and access to offline least squares and log loss regression oracles. Our algorithm is efficient (assuming efficient offline regression oracles) and enjoys an $\widetilde{O}(H^3 \sqrt{T |S| |A|(\log (|\mathcal{F}|/\delta) + \log (|\mathcal{P}|/ \delta) )})$ regret guarantee, with $T$ being the number of episodes, $S$ the state space, $A$ the action space, $H$ the horizon, and $\mathcal{P}$ and $\mathcal{F}$ are finite function classes, used to approximate the context-dependent dynamics and rewards, respectively. To the best of our knowledge, our algorithm is the first efficient and rate-optimal regret minimization algorithm for CMDPs, which operates under the general offline function approximation setting.

Optimism in Face of a Context: Regret Guarantees for Stochastic Contextual MDP

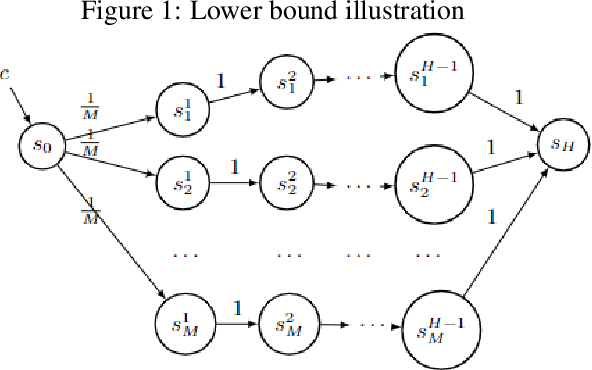
We present regret minimization algorithms for stochastic contextual MDPs under minimum reachability assumption, using an access to an offline least square regression oracle. We analyze three different settings: where the dynamics is known, where the dynamics is unknown but independent of the context and the most challenging setting where the dynamics is unknown and context-dependent. For the latter, our algorithm obtains $ \tilde{O}\left( \max\{H,{1}/{p_{min}}\}H|S|^{3/2}\sqrt{|A|T\log(\max\{|\mathcal{F}|,|\mathcal{P}|\}/\delta)} \right)$ regret bound, with probability $1-\delta$, where $\mathcal{P}$ and $\mathcal{F}$ are finite and realizable function classes used to approximate the dynamics and rewards respectively, $p_{min}$ is the minimum reachability parameter, $S$ is the set of states, $A$ the set of actions, $H$ the horizon, and $T$ the number of episodes. To our knowledge, our approach is the first optimistic approach applied to contextual MDPs with general function approximation (i.e., without additional knowledge regarding the function class, such as it being linear and etc.). In addition, we present a lower bound of $\Omega(\sqrt{T H |S| |A| \ln(|\mathcal{F}|/|S|)/\ln(|A|)})$, on the expected regret which holds even in the case of known dynamics.

Learning Efficiently Function Approximation for Contextual MDP

We study learning contextual MDPs using a function approximation for both the rewards and the dynamics. We consider both the case where the dynamics is known and unknown, and the case that the dynamics dependent or independent of the context. For all four models we derive polynomial sample and time complexity (assuming an efficient ERM oracle). Our methodology gives a general reduction from learning contextual MDP to supervised learning.