An Improved Best-of-both-worlds Algorithm for Bandits with Delayed Feedback

We propose a new best-of-both-worlds algorithm for bandits with variably delayed feedback. The algorithm improves on prior work by Masoudian et al. [2022] by eliminating the need in prior knowledge of the maximal delay $d_{\mathrm{max}}$ and providing tighter regret bounds in both regimes. The algorithm and its regret bounds are based on counts of outstanding observations (a quantity that is observed at action time) rather than delays or the maximal delay (quantities that are only observed when feedback arrives). One major contribution is a novel control of distribution drift, which is based on biased loss estimators and skipping of observations with excessively large delays. Another major contribution is demonstrating that the complexity of best-of-both-worlds bandits with delayed feedback is characterized by the cumulative count of outstanding observations after skipping of observations with excessively large delays, rather than the delays or the maximal delay.

Delayed Bandits: When Do Intermediate Observations Help?

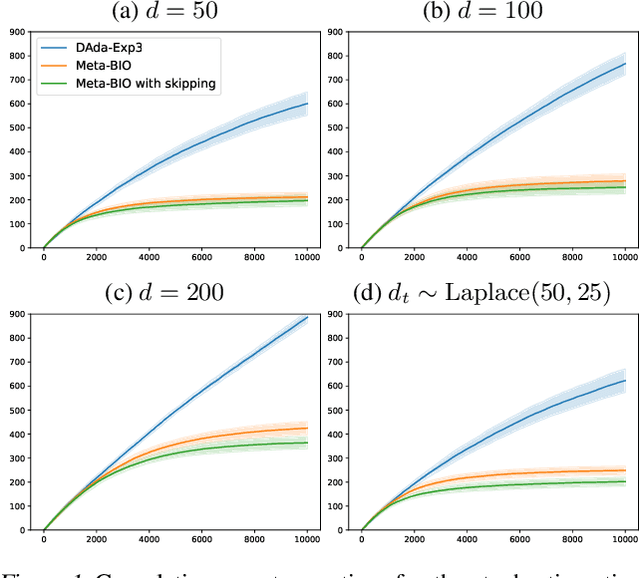
We study a $K$-armed bandit with delayed feedback and intermediate observations. We consider a model where intermediate observations have a form of a finite state, which is observed immediately after taking an action, whereas the loss is observed after an adversarially chosen delay. We show that the regime of the mapping of states to losses determines the complexity of the problem, irrespective of whether the mapping of actions to states is stochastic or adversarial. If the mapping of states to losses is adversarial, then the regret rate is of order $\sqrt{(K+d)T}$ (within log factors), where $T$ is the time horizon and $d$ is a fixed delay. This matches the regret rate of a $K$-armed bandit with delayed feedback and without intermediate observations, implying that intermediate observations are not helpful. However, if the mapping of states to losses is stochastic, we show that the regret grows at a rate of $\sqrt{\big(K+\min\{|\mathcal{S}|,d\}\big)T}$ (within log factors), implying that if the number $|\mathcal{S}|$ of states is smaller than the delay, then intermediate observations help. We also provide refined high-probability regret upper bounds for non-uniform delays, together with experimental validation of our algorithms.

A Best-of-Both-Worlds Algorithm for Bandits with Delayed Feedback

We present a modified tuning of the algorithm of Zimmert and Seldin [2020] for adversarial multiarmed bandits with delayed feedback, which in addition to the minimax optimal adversarial regret guarantee shown by Zimmert and Seldin simultaneously achieves a near-optimal regret guarantee in the stochastic setting with fixed delays. Specifically, the adversarial regret guarantee is $\mathcal{O}(\sqrt{TK} + \sqrt{dT\log K})$, where $T$ is the time horizon, $K$ is the number of arms, and $d$ is the fixed delay, whereas the stochastic regret guarantee is $\mathcal{O}\left(\sum_{i \neq i^*}(\frac{1}{\Delta_i} \log(T) + \frac{d}{\Delta_{i}\log K}) + d K^{1/3}\log K\right)$, where $\Delta_i$ are the suboptimality gaps. We also present an extension of the algorithm to the case of arbitrary delays, which is based on an oracle knowledge of the maximal delay $d_{max}$ and achieves $\mathcal{O}(\sqrt{TK} + \sqrt{D\log K} + d_{max}K^{1/3} \log K)$ regret in the adversarial regime, where $D$ is the total delay, and $\mathcal{O}\left(\sum_{i \neq i^*}(\frac{1}{\Delta_i} \log(T) + \frac{\sigma_{max}}{\Delta_{i}\log K}) + d_{max}K^{1/3}\log K\right)$ regret in the stochastic regime, where $\sigma_{max}$ is the maximal number of outstanding observations. Finally, we present a lower bound that matches regret upper bound achieved by the skipping technique of Zimmert and Seldin [2020] in the adversarial setting.

Improved Analysis of Robustness of the Tsallis-INF Algorithm to Adversarial Corruptions in Stochastic Multiarmed Bandits

We derive improved regret bounds for the Tsallis-INF algorithm of Zimmert and Seldin (2021). In the adversarial regime with a self-bounding constraint and the stochastic regime with adversarial corruptions as its special case we improve the dependence on corruption magnitude $C$. In particular, for $C = \Theta\left(\frac{T}{\log T}\right)$, where $T$ is the time horizon, we achieve an improvement by a multiplicative factor of $\sqrt{\frac{\log T}{\log\log T}}$ relative to the bound of Zimmert and Seldin (2021). We also improve the dependence of the regret bound on time horizon from $\log T$ to $\log \frac{(K-1)T}{(\sum_{i\neq i^*}\frac{1}{\Delta_i})^2}$, where $K$ is the number of arms, $\Delta_i$ are suboptimality gaps for suboptimal arms $i$, and $i^*$ is the optimal arm. Additionally, we provide a general analysis, which allows to achieve the same kind of improvement for generalizations of Tsallis-INF to other settings beyond multiarmed bandits.

Accurate and Rapid Diagnosis of COVID-19 Pneumonia with Batch Effect Removal of Chest CT-Scans and Interpretable Artificial Intelligence

Since late 2019, COVID-19 has been spreading over the world and caused the death of many people. The high transmission rate of the virus demands the rapid identification of infected patients to reduce the spread of the disease. The current gold-standard test, Reverse-Transcription Polymerase Chain Reaction (RT-PCR), suffers from a high rate of false negatives. Diagnosis from CT-scan images as an alternative with higher accuracy and sensitivity has the challenge of distinguishing COVID-19 from other lung diseases which demand expert radiologists. In peak times, artificial intelligence (AI) based diagnostic systems can help radiologists to accelerate the process of diagnosis, increase the accuracy, and understand the severity of the disease. We designed an interpretable deep neural network to distinguish healthy people, patients with COVID-19, and patients with other lung diseases from chest CT-scan images. Our model also detects the infected areas of the lung and is able to calculate the percentage of the infected volume. We preprocessed the images to eliminate the batch effect related to CT-scan devices and medical centers and then adopted a weakly supervised method to train the model without having any label for infected parts and any tags for the slices of the CT-scan images that had signs of disease. We trained and evaluated the model on a large dataset of 3359 CT-scan images from 6 medical centers. The model reached a sensitivity of 97.75% and a specificity of 87% in separating healthy people from the diseased and a sensitivity of 98.15% and a specificity of 81.03% in distinguishing COVID-19 from other diseases. The model also reached similar metrics in 1435 samples from 6 unseen medical centers that prove its generalizability. The performance of the model on a large diverse dataset, its generalizability, and interpretability makes it suitable to be used as a diagnostic system.

Adaptive Online Learning for Gradient-Based Optimizers

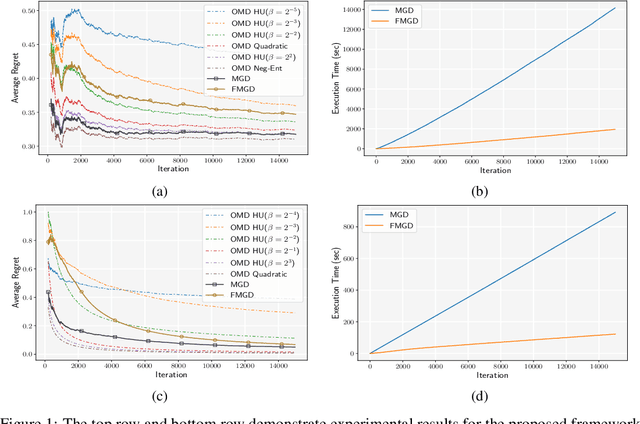
As application demands for online convex optimization accelerate, the need for designing new methods that simultaneously cover a large class of convex functions and impose the lowest possible regret is highly rising. Known online optimization methods usually perform well only in specific settings, and their performance depends highly on the geometry of the decision space and cost functions. However, in practice, lack of such geometric information leads to confusion in using the appropriate algorithm. To address this issue, some adaptive methods have been proposed that focus on adaptively learning parameters such as step size, Lipschitz constant, and strong convexity coefficient, or on specific parametric families such as quadratic regularizers. In this work, we generalize these methods and propose a framework that competes with the best algorithm in a family of expert algorithms. Our framework includes many of the well-known adaptive methods including MetaGrad, MetaGrad+C, and Ader. We also introduce a second algorithm that computationally outperforms our first algorithm with at most a constant factor increase in regret. Finally, as a representative application of our proposed algorithm, we study the problem of learning the best regularizer from a family of regularizers for Online Mirror Descent. Empirically, we support our theoretical findings in the problem of learning the best regularizer on the simplex and $l_2$-ball in a multiclass learning problem.