Federated $\mathcal{X}$-armed Bandit with Flexible Personalisation

This paper introduces a novel approach to personalised federated learning within the $\mathcal{X}$-armed bandit framework, addressing the challenge of optimising both local and global objectives in a highly heterogeneous environment. Our method employs a surrogate objective function that combines individual client preferences with aggregated global knowledge, allowing for a flexible trade-off between personalisation and collective learning. We propose a phase-based elimination algorithm that achieves sublinear regret with logarithmic communication overhead, making it well-suited for federated settings. Theoretical analysis and empirical evaluations demonstrate the effectiveness of our approach compared to existing methods. Potential applications of this work span various domains, including healthcare, smart home devices, and e-commerce, where balancing personalisation with global insights is crucial.

Adaptive Online Learning for Gradient-Based Optimizers

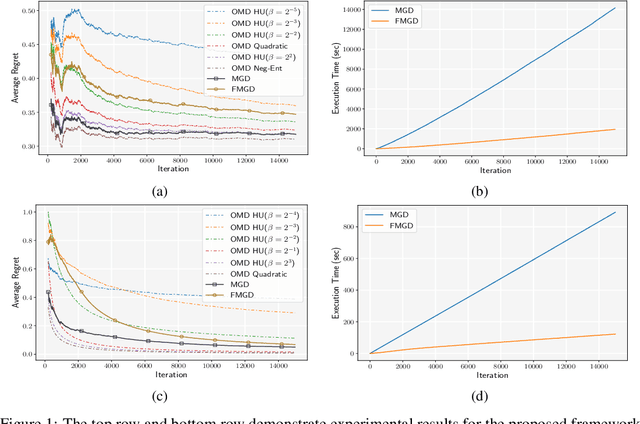
As application demands for online convex optimization accelerate, the need for designing new methods that simultaneously cover a large class of convex functions and impose the lowest possible regret is highly rising. Known online optimization methods usually perform well only in specific settings, and their performance depends highly on the geometry of the decision space and cost functions. However, in practice, lack of such geometric information leads to confusion in using the appropriate algorithm. To address this issue, some adaptive methods have been proposed that focus on adaptively learning parameters such as step size, Lipschitz constant, and strong convexity coefficient, or on specific parametric families such as quadratic regularizers. In this work, we generalize these methods and propose a framework that competes with the best algorithm in a family of expert algorithms. Our framework includes many of the well-known adaptive methods including MetaGrad, MetaGrad+C, and Ader. We also introduce a second algorithm that computationally outperforms our first algorithm with at most a constant factor increase in regret. Finally, as a representative application of our proposed algorithm, we study the problem of learning the best regularizer from a family of regularizers for Online Mirror Descent. Empirically, we support our theoretical findings in the problem of learning the best regularizer on the simplex and $l_2$-ball in a multiclass learning problem.

Recurrent Poisson Factorization for Temporal Recommendation

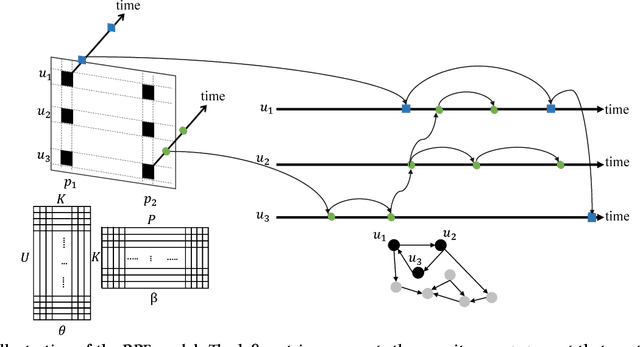
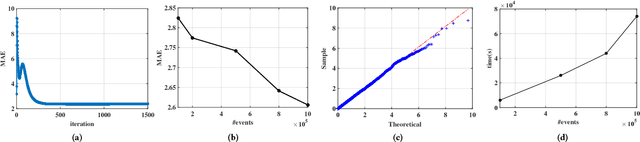
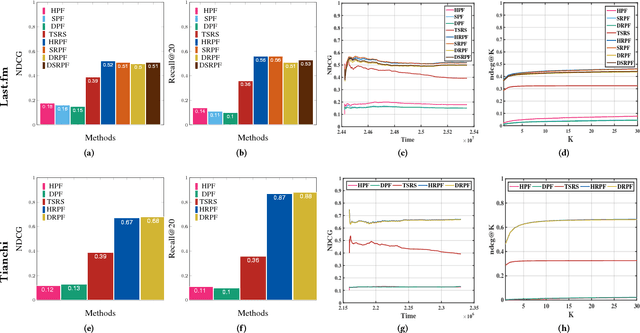
Poisson factorization is a probabilistic model of users and items for recommendation systems, where the so-called implicit consumer data is modeled by a factorized Poisson distribution. There are many variants of Poisson factorization methods who show state-of-the-art performance on real-world recommendation tasks. However, most of them do not explicitly take into account the temporal behavior and the recurrent activities of users which is essential to recommend the right item to the right user at the right time. In this paper, we introduce Recurrent Poisson Factorization (RPF) framework that generalizes the classical PF methods by utilizing a Poisson process for modeling the implicit feedback. RPF treats time as a natural constituent of the model and brings to the table a rich family of time-sensitive factorization models. To elaborate, we instantiate several variants of RPF who are capable of handling dynamic user preferences and item specification (DRPF), modeling the social-aspect of product adoption (SRPF), and capturing the consumption heterogeneity among users and items (HRPF). We also develop a variational algorithm for approximate posterior inference that scales up to massive data sets. Furthermore, we demonstrate RPF's superior performance over many state-of-the-art methods on synthetic dataset, and large scale real-world datasets on music streaming logs, and user-item interactions in M-Commerce platforms.