Federated $\mathcal{X}$-armed Bandit with Flexible Personalisation

This paper introduces a novel approach to personalised federated learning within the $\mathcal{X}$-armed bandit framework, addressing the challenge of optimising both local and global objectives in a highly heterogeneous environment. Our method employs a surrogate objective function that combines individual client preferences with aggregated global knowledge, allowing for a flexible trade-off between personalisation and collective learning. We propose a phase-based elimination algorithm that achieves sublinear regret with logarithmic communication overhead, making it well-suited for federated settings. Theoretical analysis and empirical evaluations demonstrate the effectiveness of our approach compared to existing methods. Potential applications of this work span various domains, including healthcare, smart home devices, and e-commerce, where balancing personalisation with global insights is crucial.

Apple Tasting Revisited: Bayesian Approaches to Partially Monitored Online Binary Classification

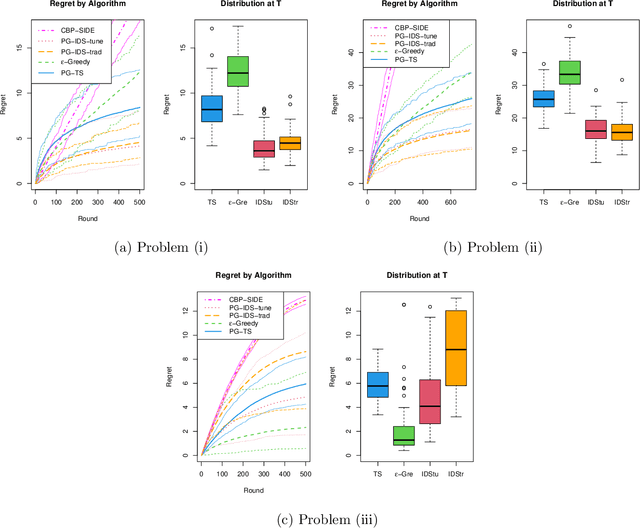
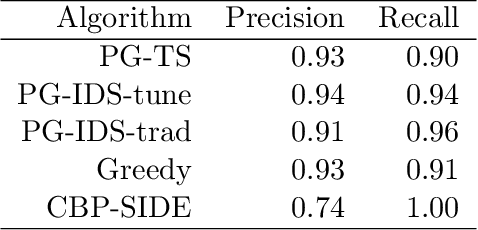
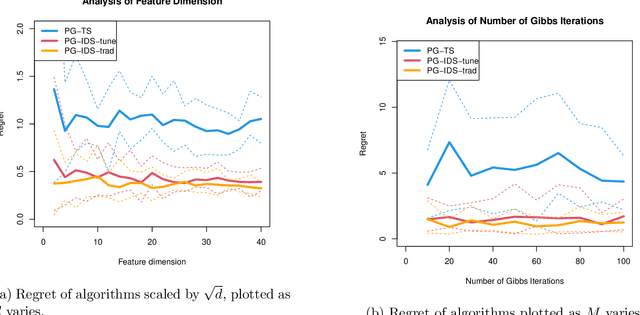
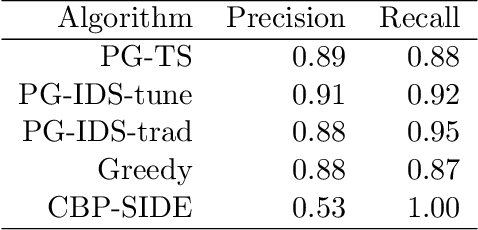
We consider a variant of online binary classification where a learner sequentially assigns labels ($0$ or $1$) to items with unknown true class. If, but only if, the learner chooses label $1$ they immediately observe the true label of the item. The learner faces a trade-off between short-term classification accuracy and long-term information gain. This problem has previously been studied under the name of the `apple tasting' problem. We revisit this problem as a partial monitoring problem with side information, and focus on the case where item features are linked to true classes via a logistic regression model. Our principal contribution is a study of the performance of Thompson Sampling (TS) for this problem. Using recently developed information-theoretic tools, we show that TS achieves a Bayesian regret bound of an improved order to previous approaches. Further, we experimentally verify that efficient approximations to TS and Information Directed Sampling via P\'{o}lya-Gamma augmentation have superior empirical performance to existing methods.

Learning to Rank under Multinomial Logit Choice

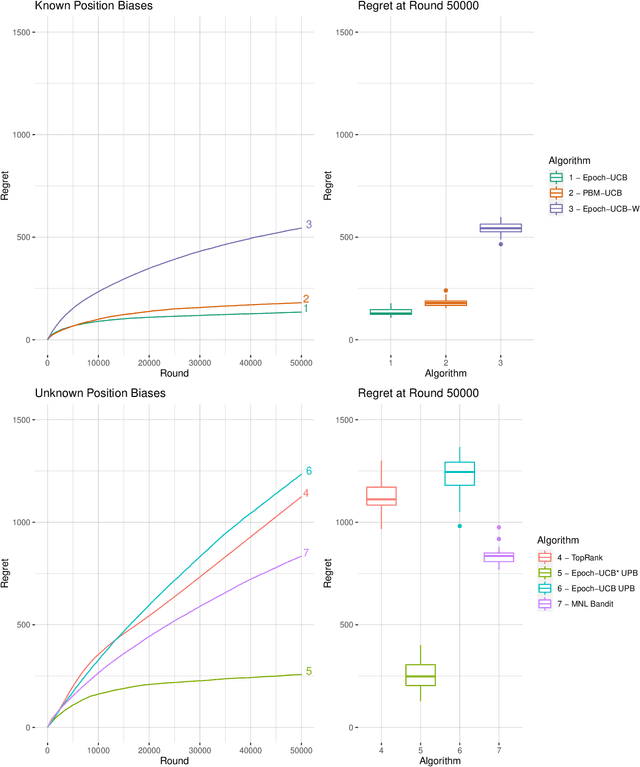
Learning the optimal ordering of content is an important challenge in website design. The learning to rank (LTR) framework models this problem as a sequential problem of selecting lists of content and observing where users decide to click. Most previous work on LTR assumes that the user considers each item in the list in isolation, and makes binary choices to click or not on each. We introduce a multinomial logit (MNL) choice model to the LTR framework, which captures the behaviour of users who consider the ordered list of items as a whole and make a single choice among all the items and a no-click option. Under the MNL model, the user favours items which are either inherently more attractive, or placed in a preferable position within the list. We propose upper confidence bound algorithms to minimise regret in two settings - where the position dependent parameters are known, and unknown. We present theoretical analysis leading to an $\Omega(\sqrt{T})$ lower bound for the problem, an $\tilde{O}(\sqrt{T})$ upper bound on regret for the known parameter version. Our analyses are based on tight new concentration results for Geometric random variables, and novel functional inequalities for maximum likelihood estimators computed on discrete data.

Filtered Poisson Process Bandit on a Continuum

We consider a version of the continuum armed bandit where an action induces a filtered realisation of a non-homogeneous Poisson process. Point data in the filtered sample are then revealed to the decision-maker, whose reward is the total number of revealed points. Using knowledge of the function governing the filtering, but without knowledge of the Poisson intensity function, the decision-maker seeks to maximise the expected number of revealed points over T rounds. We propose an upper confidence bound algorithm for this problem utilising data-adaptive discretisation of the action space. This approach enjoys O(T^(2/3)) regret under a Lipschitz assumption on the reward function. We provide lower bounds on the regret of any algorithm for the problem, via new lower bounds for related finite-armed bandits, and show that the orders of the upper and lower bounds match up to a logarithmic factor.

On Thompson Sampling for Smoother-than-Lipschitz Bandits

Thompson Sampling is a well established approach to bandit and reinforcement learning problems. However its use in continuum armed bandit problems has received relatively little attention. We provide the first bounds on the regret of Thompson Sampling for continuum armed bandits under weak conditions on the function class containing the true function and sub-exponential observation noise. Our bounds are realised by analysis of the eluder dimension, a recently proposed measure of the complexity of a function class, which has been demonstrated to be useful in bounding the Bayesian regret of Thompson Sampling for simpler bandit problems under sub-Gaussian observation noise. We derive a new bound on the eluder dimension for classes of functions with Lipschitz derivatives, and generalise previous analyses in multiple regards.

Combinatorial Multi-Armed Bandits with Filtered Feedback

Motivated by problems in search and detection we present a solution to a Combinatorial Multi-Armed Bandit (CMAB) problem with both heavy-tailed reward distributions and a new class of feedback, filtered semibandit feedback. In a CMAB problem an agent pulls a combination of arms from a set $\{1,...,k\}$ in each round, generating random outcomes from probability distributions associated with these arms and receiving an overall reward. Under semibandit feedback it is assumed that the random outcomes generated are all observed. Filtered semibandit feedback allows the outcomes that are observed to be sampled from a second distribution conditioned on the initial random outcomes. This feedback mechanism is valuable as it allows CMAB methods to be applied to sequential search and detection problems where combinatorial actions are made, but the true rewards (number of objects of interest appearing in the round) are not observed, rather a filtered reward (the number of objects the searcher successfully finds, which must by definition be less than the number that appear). We present an upper confidence bound type algorithm, Robust-F-CUCB, and associated regret bound of order $\mathcal{O}(\ln(n))$ to balance exploration and exploitation in the face of both filtering of reward and heavy tailed reward distributions.