Learning to Rank under Multinomial Logit Choice

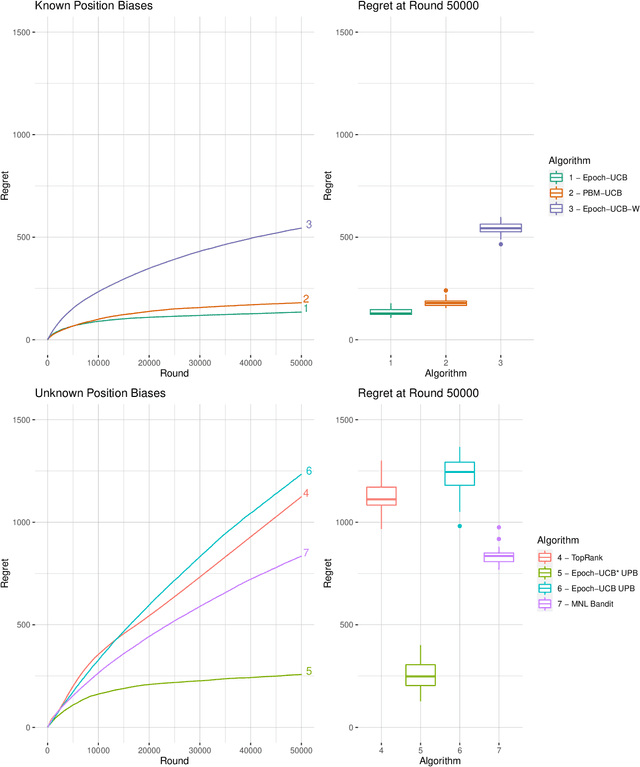
Learning the optimal ordering of content is an important challenge in website design. The learning to rank (LTR) framework models this problem as a sequential problem of selecting lists of content and observing where users decide to click. Most previous work on LTR assumes that the user considers each item in the list in isolation, and makes binary choices to click or not on each. We introduce a multinomial logit (MNL) choice model to the LTR framework, which captures the behaviour of users who consider the ordered list of items as a whole and make a single choice among all the items and a no-click option. Under the MNL model, the user favours items which are either inherently more attractive, or placed in a preferable position within the list. We propose upper confidence bound algorithms to minimise regret in two settings - where the position dependent parameters are known, and unknown. We present theoretical analysis leading to an $\Omega(\sqrt{T})$ lower bound for the problem, an $\tilde{O}(\sqrt{T})$ upper bound on regret for the known parameter version. Our analyses are based on tight new concentration results for Geometric random variables, and novel functional inequalities for maximum likelihood estimators computed on discrete data.