On Margin-Based Cluster Recovery with Oracle Queries
Paper and Code
Jun 09, 2021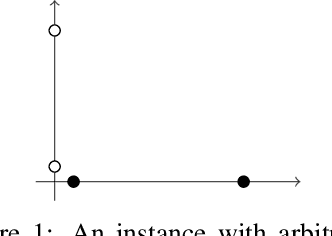
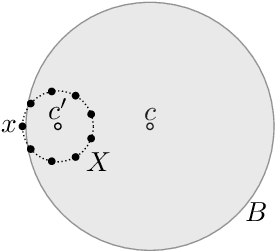
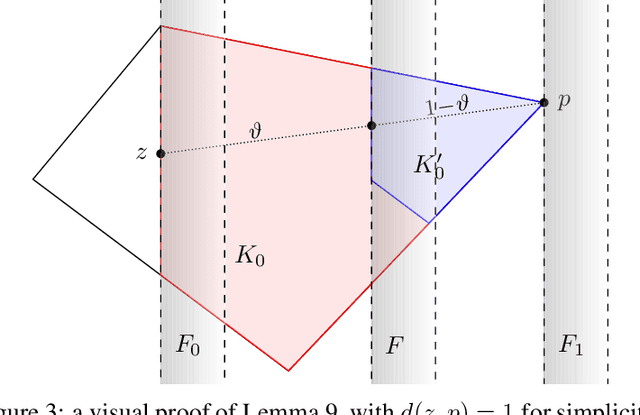
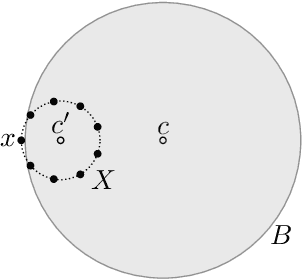
We study an active cluster recovery problem where, given a set of $n$ points and an oracle answering queries like "are these two points in the same cluster?", the task is to recover exactly all clusters using as few queries as possible. We begin by introducing a simple but general notion of margin between clusters that captures, as special cases, the margins used in previous work, the classic SVM margin, and standard notions of stability for center-based clusterings. Then, under our margin assumptions we design algorithms that, in a variety of settings, recover all clusters exactly using only $O(\log n)$ queries. For the Euclidean case, $\mathbb{R}^m$, we give an algorithm that recovers arbitrary convex clusters, in polynomial time, and with a number of queries that is lower than the best existing algorithm by $\Theta(m^m)$ factors. For general pseudometric spaces, where clusters might not be convex or might not have any notion of shape, we give an algorithm that achieves the $O(\log n)$ query bound, and is provably near-optimal as a function of the packing number of the space. Finally, for clusterings realized by binary concept classes, we give a combinatorial characterization of recoverability with $O(\log n)$ queries, and we show that, for many concept classes in Euclidean spaces, this characterization is equivalent to our margin condition. Our results show a deep connection between cluster margins and active cluster recoverability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge