Bandit and Delayed Feedback in Online Structured Prediction

Online structured prediction is a task of sequentially predicting outputs with complex structures based on inputs and past observations, encompassing online classification. Recent studies showed that in the full information setup, we can achieve finite bounds on the surrogate regret, i.e., the extra target loss relative to the best possible surrogate loss. In practice, however, full information feedback is often unrealistic as it requires immediate access to the whole structure of complex outputs. Motivated by this, we propose algorithms that work with less demanding feedback, bandit and delayed feedback. For the bandit setting, using a standard inverse-weighted gradient estimator, we achieve a surrogate regret bound of $O(\sqrt{KT})$ for the time horizon $T$ and the size of the output set $K$. However, $K$ can be extremely large when outputs are highly complex, making this result less desirable. To address this, we propose an algorithm that achieves a surrogate regret bound of $O(T^{2/3})$, which is independent of $K$. This is enabled with a carefully designed pseudo-inverse matrix estimator. Furthermore, for the delayed full information feedback setup, we obtain a surrogate regret bound of $O(D^{2/3} T^{1/3})$ for the delay time $D$. We also provide algorithms for the delayed bandit feedback setup. Finally, we numerically evaluate the performance of the proposed algorithms in online classification with bandit feedback.

Instance-Dependent Regret Bounds for Learning Two-Player Zero-Sum Games with Bandit Feedback

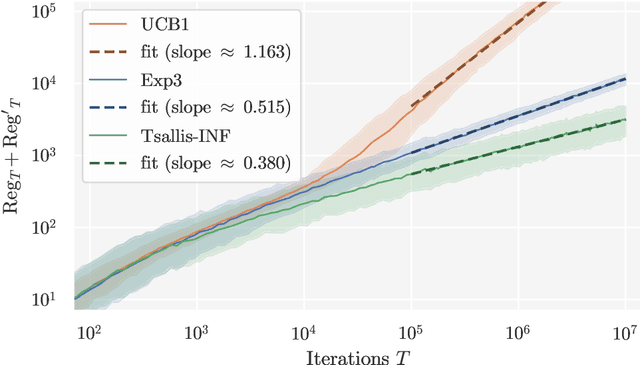
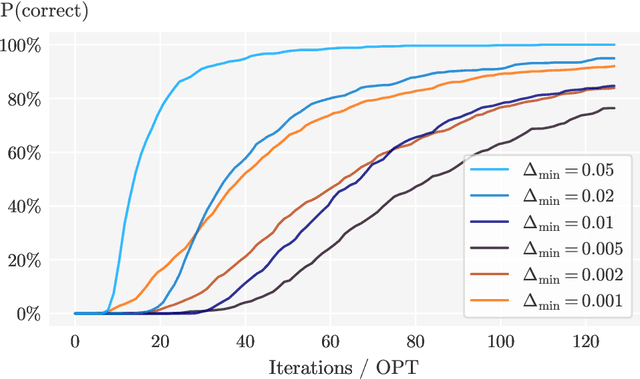
No-regret self-play learning dynamics have become one of the premier ways to solve large-scale games in practice. Accelerating their convergence via improving the regret of the players over the naive $O(\sqrt{T})$ bound after $T$ rounds has been extensively studied in recent years, but almost all studies assume access to exact gradient feedback. We address the question of whether acceleration is possible under bandit feedback only and provide an affirmative answer for two-player zero-sum normal-form games. Specifically, we show that if both players apply the Tsallis-INF algorithm of Zimmert and Seldin (2018, arXiv:1807.07623), then their regret is at most $O(c_1 \log T + \sqrt{c_2 T})$, where $c_1$ and $c_2$ are game-dependent constants that characterize the difficulty of learning -- $c_1$ resembles the complexity of learning a stochastic multi-armed bandit instance and depends inversely on some gap measures, while $c_2$ can be much smaller than the number of actions when the Nash equilibria have a small support or are close to the boundary. In particular, for the case when a pure strategy Nash equilibrium exists, $c_2$ becomes zero, leading to an optimal instance-dependent regret bound as we show. We additionally prove that in this case, our algorithm also enjoys last-iterate convergence and can identify the pure strategy Nash equilibrium with near-optimal sample complexity.

Online Inverse Linear Optimization: Improved Regret Bound, Robustness to Suboptimality, and Toward Tight Regret Analysis

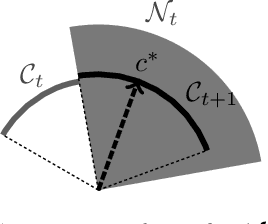
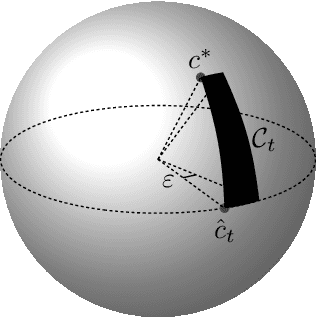
We study an online learning problem where, over $T$ rounds, a learner observes both time-varying sets of feasible actions and an agent's optimal actions, selected by solving linear optimization over the feasible actions. The learner sequentially makes predictions of the agent's underlying linear objective function, and their quality is measured by the regret, the cumulative gap between optimal objective values and those achieved by following the learner's predictions. A seminal work by B\"armann et al. (ICML 2017) showed that online learning methods can be applied to this problem to achieve regret bounds of $O(\sqrt{T})$. Recently, Besbes et al. (COLT 2021, Oper. Res. 2023) significantly improved the result by achieving an $O(n^4\ln T)$ regret bound, where $n$ is the dimension of the ambient space of objective vectors. Their method, based on the ellipsoid method, runs in polynomial time but is inefficient for large $n$ and $T$. In this paper, we obtain an $O(n\ln T)$ regret bound, improving upon the previous bound of $O(n^4\ln T)$ by a factor of $n^3$. Our method is simple and efficient: we apply the online Newton step (ONS) to appropriate exp-concave loss functions. Moreover, for the case where the agent's actions are possibly suboptimal, we establish an $O(n\ln T+\sqrt{\Delta_Tn\ln T})$ regret bound, where $\Delta_T$ is the cumulative suboptimality of the agent's actions. This bound is achieved by using MetaGrad, which runs ONS with $\Theta(\ln T)$ different learning rates in parallel. We also provide a simple instance that implies an $\Omega(n)$ lower bound, showing that our $O(n\ln T)$ bound is tight up to an $O(\ln T)$ factor. This gives rise to a natural question: can the $O(\ln T)$ factor in the upper bound be removed? For the special case of $n=2$, we show that an $O(1)$ regret bound is possible, while we delineate challenges in extending this result to higher dimensions.

Revisiting Online Learning Approach to Inverse Linear Optimization: A Fenchel$-$Young Loss Perspective and Gap-Dependent Regret Analysis

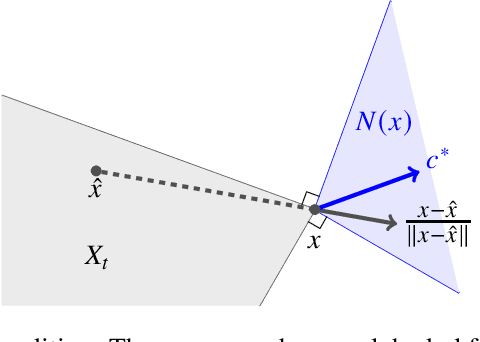
This paper revisits the online learning approach to inverse linear optimization studied by B\"armann et al. (2017), where the goal is to infer an unknown linear objective function of an agent from sequential observations of the agent's input-output pairs. First, we provide a simple understanding of the online learning approach through its connection to online convex optimization of \emph{Fenchel--Young losses}. As a byproduct, we present an offline guarantee on the \emph{suboptimality loss}, which measures how well predicted objectives explain the agent's choices, without assuming the optimality of the agent's choices. Second, assuming that there is a gap between optimal and suboptimal objective values in the agent's decision problems, we obtain an upper bound independent of the time horizon $T$ on the sum of suboptimality and \emph{estimate losses}, where the latter measures the quality of solutions recommended by predicted objectives. Interestingly, our gap-dependent analysis achieves a faster rate than the standard $O(\sqrt{T})$ regret bound by exploiting structures specific to inverse linear optimization, even though neither the loss functions nor their domains enjoy desirable properties, such as strong convexity.

Corrupted Learning Dynamics in Games

Learning in games is the problem where multiple players interact in a shared environment, each aiming to minimize their own regret, and it is known that an approximate equilibrium can be obtained when all players employ no-regret algorithms. Notably, by adopting optimistic follow-the-regularized-leader (OFTRL), the regret of each player after $T$ rounds is constant in two-player zero-sum games, implying that an equilibrium can be computed at a faster rate of $O(1/T)$. However, this acceleration is limited to the honest regime, where all players fully adhere to the given algorithms. To address this limitation, this paper presents corrupted learning dynamics that adaptively find an equilibrium at a rate dependent on the degree of deviation by each player from the given algorithm's output. First, in two-player zero-sum games, we provide learning dynamics where the external regret of the x-player (and similarly for the y-player) in the corrupted regime is roughly bounded by $O(\log (m_\mathrm{x} m_\mathrm{y}) + \sqrt{C_\mathrm{y}} + C_\mathrm{x})$, which implies a convergence rate of $\tilde{O}((\sqrt{C_\mathrm{y}} + C_\mathrm{x})/T)$ to a Nash equilibrium. Here, $m_\mathrm{x}$ and $m_\mathrm{y}$ are the number of actions of the x- and y-players, respectively, and $C_\mathrm{x}$ and $C_\mathrm{y}$ are the cumulative deviations of the x- and y-players from their given algorithms. Furthermore, we extend our approach to multi-player general-sum games, showing that the swap regret of player $i$ in the corrupted regime is bounded by $O(\log T + \sqrt{\sum_j C_j \log T} + C_i)$, where $C_i$ is the cumulative deviations of player $i$ from the given algorithm. This implies a convergence rate of $O((\log T + \sqrt{\sum_j C_j \log T} + C_i)/T)$ to a correlated equilibrium. Our learning dynamics are agnostic to the corruption levels and are based on OFTRL with new adaptive learning rates.

A Simple and Adaptive Learning Rate for FTRL in Online Learning with Minimax Regret of $Θ$ and its Application to Best-of-Both-Worlds

Follow-the-Regularized-Leader (FTRL) is a powerful framework for various online learning problems. By designing its regularizer and learning rate to be adaptive to past observations, FTRL is known to work adaptively to various properties of an underlying environment. However, most existing adaptive learning rates are for online learning problems with a minimax regret of $\Theta(\sqrt{T})$ for the number of rounds $T$, and there are only a few studies on adaptive learning rates for problems with a minimax regret of $\Theta(T^{2/3})$, which include several important problems dealing with indirect feedback. To address this limitation, we establish a new adaptive learning rate framework for problems with a minimax regret of $\Theta(T^{2/3})$. Our learning rate is designed by matching the stability, penalty, and bias terms that naturally appear in regret upper bounds for problems with a minimax regret of $\Theta(T^{2/3})$. As applications of this framework, we consider two major problems dealing with indirect feedback: partial monitoring and graph bandits. We show that FTRL with our learning rate and the Tsallis entropy regularizer improves existing Best-of-Both-Worlds (BOBW) regret upper bounds, which achieve simultaneous optimality in the stochastic and adversarial regimes. The resulting learning rate is surprisingly simple compared to the existing learning rates for BOBW algorithms for problems with a minimax regret of $\Theta(T^{2/3})$.

Adaptive Learning Rate for Follow-the-Regularized-Leader: Competitive Analysis and Best-of-Both-Worlds

Follow-The-Regularized-Leader (FTRL) is known as an effective and versatile approach in online learning, where appropriate choice of the learning rate is crucial for smaller regret. To this end, we formulate the problem of adjusting FTRL's learning rate as a sequential decision-making problem and introduce the framework of competitive analysis. We establish a lower bound for the competitive ratio and propose update rules for learning rate that achieves an upper bound within a constant factor of this lower bound. Specifically, we illustrate that the optimal competitive ratio is characterized by the (approximate) monotonicity of components of the penalty term, showing that a constant competitive ratio is achievable if the components of the penalty term form a monotonically non-increasing sequence, and derive a tight competitive ratio when penalty terms are $\xi$-approximately monotone non-increasing. Our proposed update rule, referred to as \textit{stability-penalty matching}, also facilitates constructing the Best-Of-Both-Worlds (BOBW) algorithms for stochastic and adversarial environments. In these environments our result contributes to achieve tighter regret bound and broaden the applicability of algorithms for various settings such as multi-armed bandits, graph bandits, linear bandits, and contextual bandits.

Fast Rates in Online Convex Optimization by Exploiting the Curvature of Feasible Sets

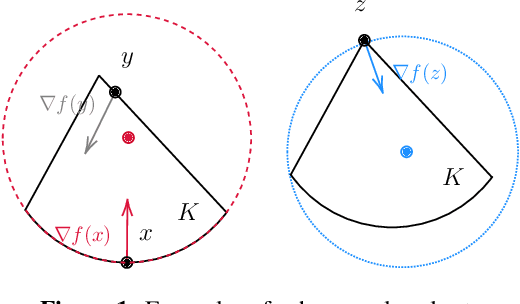
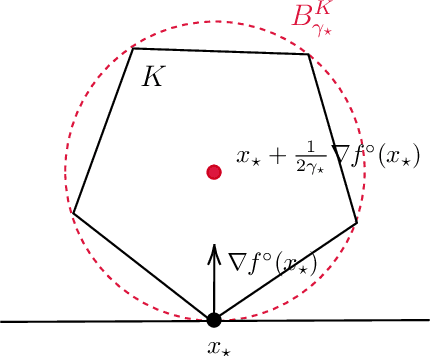
In this paper, we explore online convex optimization (OCO) and introduce a new analysis that provides fast rates by exploiting the curvature of feasible sets. In online linear optimization, it is known that if the average gradient of loss functions is larger than a certain value, the curvature of feasible sets can be exploited by the follow-the-leader (FTL) algorithm to achieve a logarithmic regret. This paper reveals that algorithms adaptive to the curvature of loss functions can also leverage the curvature of feasible sets. We first prove that if an optimal decision is on the boundary of a feasible set and the gradient of an underlying loss function is non-zero, then the algorithm achieves a regret upper bound of $O(\rho \log T)$ in stochastic environments. Here, $\rho > 0$ is the radius of the smallest sphere that includes the optimal decision and encloses the feasible set. Our approach, unlike existing ones, can work directly with convex loss functions, exploiting the curvature of loss functions simultaneously, and can achieve the logarithmic regret only with a local property of feasible sets. Additionally, it achieves an $O(\sqrt{T})$ regret even in adversarial environments where FTL suffers an $\Omega(T)$ regret, and attains an $O(\rho \log T + \sqrt{C \rho \log T})$ regret bound in corrupted stochastic environments with corruption level $C$. Furthermore, by extending our analysis, we establish a regret upper bound of $O\Big(T^{\frac{q-2}{2(q-1)}} (\log T)^{\frac{q}{2(q-1)}}\Big)$ for $q$-uniformly convex feasible sets, where uniformly convex sets include strongly convex sets and $\ell_p$-balls for $p \in [1,\infty)$. This bound bridges the gap between the $O(\log T)$ regret bound for strongly convex sets ($q=2$) and the $O(\sqrt{T})$ regret bound for non-curved sets ($q\to\infty$).

Online Control of Linear Systems with Unbounded and Degenerate Noise

This paper investigates the problem of controlling a linear system under possibly unbounded and degenerate noise with unknown cost functions, known as an online control problem. In contrast to the existing work, which assumes the boundedness of noise, we reveal that for convex costs, an $ \widetilde{O}(\sqrt{T}) $ regret bound can be achieved even for unbounded noise, where $ T $ denotes the time horizon. Moreover, when the costs are strongly convex, we establish an $ O({\rm poly} (\log T)) $ regret bound without the assumption that noise covariance is non-degenerate, which has been required in the literature. The key ingredient in removing the rank assumption on noise is a system transformation associated with the noise covariance. This simultaneously enables the parameter reduction of an online control algorithm.

Online Structured Prediction with Fenchel--Young Losses and Improved Surrogate Regret for Online Multiclass Classification with Logistic Loss

This paper studies online structured prediction with full-information feedback. For online multiclass classification, van der Hoeven (2020) has obtained surrogate regret bounds independent of the time horizon, or \emph{finite}, by introducing an elegant \emph{exploit-the-surrogate-gap} framework. However, this framework has been limited to multiclass classification primarily because it relies on a classification-specific procedure for converting estimated scores to outputs. We extend the exploit-the-surrogate-gap framework to online structured prediction with \emph{Fenchel--Young losses}, a large family of surrogate losses including the logistic loss for multiclass classification, obtaining finite surrogate regret bounds in various structured prediction problems. To this end, we propose and analyze \emph{randomized decoding}, which converts estimated scores to general structured outputs. Moreover, by applying our decoding to online multiclass classification with the logistic loss, we obtain a surrogate regret bound of $O(B^2)$, where $B$ is the $\ell_2$-diameter of the domain. This bound is tight up to logarithmic factors and improves the previous bound of $O(dB^2)$ due to van der Hoeven (2020) by a factor of $d$, the number of classes.