Risk-sensitive control as inference with Rényi divergence

This paper introduces the risk-sensitive control as inference (RCaI) that extends CaI by using R\'{e}nyi divergence variational inference. RCaI is shown to be equivalent to log-probability regularized risk-sensitive control, which is an extension of the maximum entropy (MaxEnt) control. We also prove that the risk-sensitive optimal policy can be obtained by solving a soft Bellman equation, which reveals several equivalences between RCaI, MaxEnt control, the optimal posterior for CaI, and linearly-solvable control. Moreover, based on RCaI, we derive the risk-sensitive reinforcement learning (RL) methods: the policy gradient and the soft actor-critic. As the risk-sensitivity parameter vanishes, we recover the risk-neutral CaI and RL, which means that RCaI is a unifying framework. Furthermore, we give another risk-sensitive generalization of the MaxEnt control using R\'{e}nyi entropy regularization. We show that in both of our extensions, the optimal policies have the same structure even though the derivations are very different.

Online Control of Linear Systems with Unbounded and Degenerate Noise

This paper investigates the problem of controlling a linear system under possibly unbounded and degenerate noise with unknown cost functions, known as an online control problem. In contrast to the existing work, which assumes the boundedness of noise, we reveal that for convex costs, an $ \widetilde{O}(\sqrt{T}) $ regret bound can be achieved even for unbounded noise, where $ T $ denotes the time horizon. Moreover, when the costs are strongly convex, we establish an $ O({\rm poly} (\log T)) $ regret bound without the assumption that noise covariance is non-degenerate, which has been required in the literature. The key ingredient in removing the rank assumption on noise is a system transformation associated with the noise covariance. This simultaneously enables the parameter reduction of an online control algorithm.

Maximum entropy optimal density control of discrete-time linear systems and Schrödinger bridges

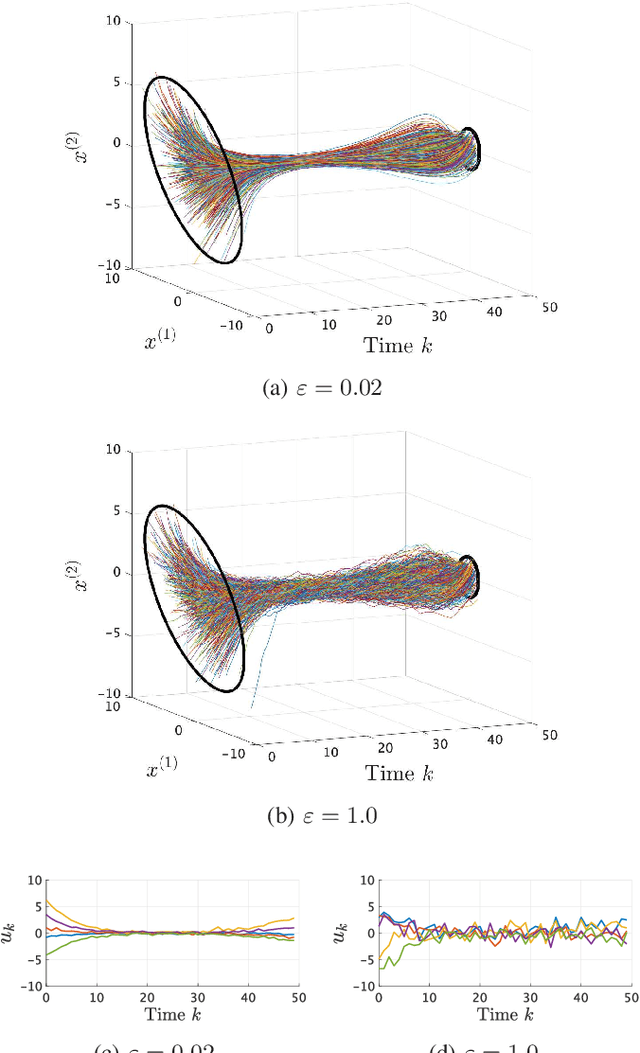
We consider an entropy-regularized version of optimal density control of deterministic discrete-time linear systems. Entropy regularization, or a maximum entropy (MaxEnt) method for optimal control has attracted much attention especially in reinforcement learning due to its many advantages such as a natural exploration strategy. Despite the merits, high-entropy control policies introduce probabilistic uncertainty into systems, which severely limits the applicability of MaxEnt optimal control to safety-critical systems. To remedy this situation, we impose a Gaussian density constraint at a specified time on the MaxEnt optimal control to directly control state uncertainty. Specifically, we derive the explicit form of the MaxEnt optimal density control. In addition, we also consider the case where a density constraint is replaced by a fixed point constraint. Then, we characterize the associated state process as a pinned process, which is a generalization of the Brownian bridge to linear systems. Finally, we reveal that the MaxEnt optimal density control induces the so-called Schr\"odinger bridge associated to a discrete-time linear system.

Kullback-Leibler control for discrete-time nonlinear systems on continuous spaces

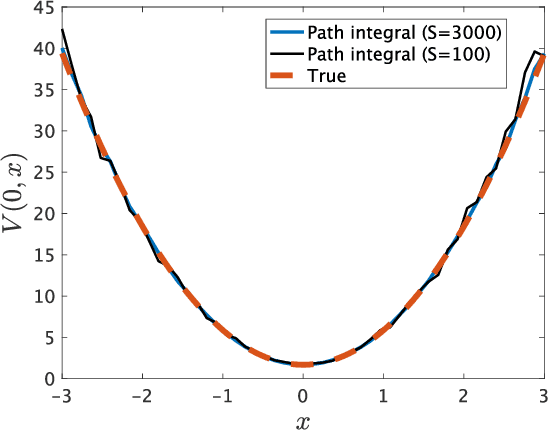
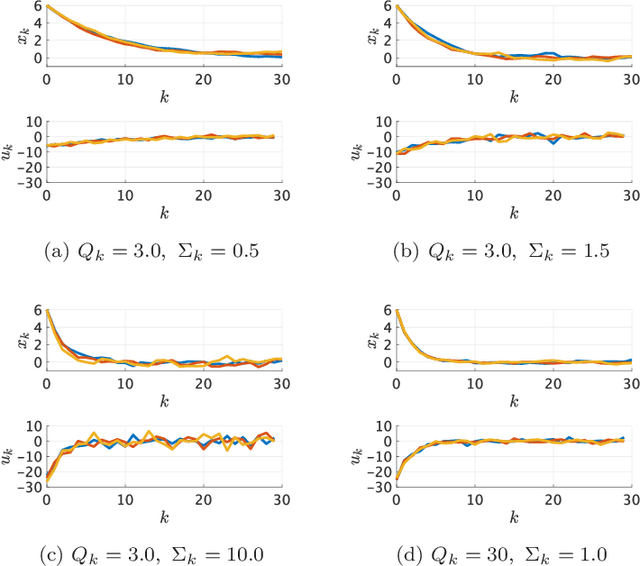
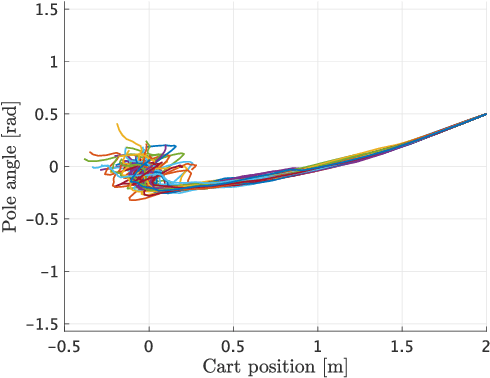
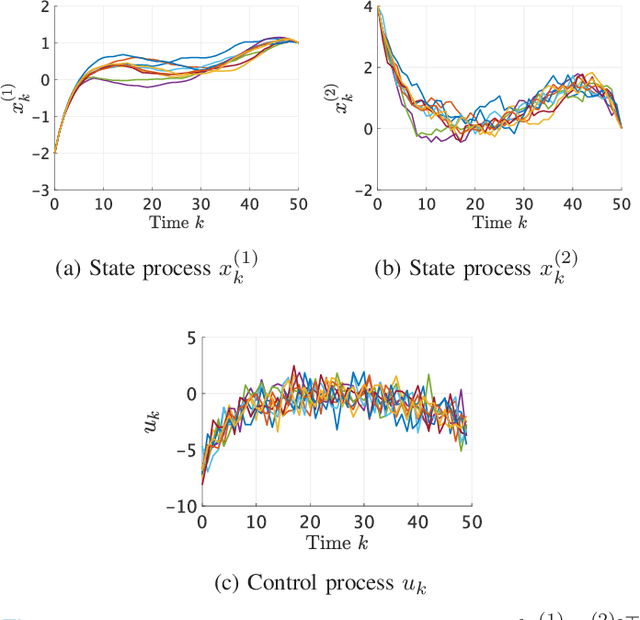
Kullback-Leibler (KL) control enables efficient numerical methods for nonlinear optimal control problems. The crucial assumption of KL control is the full controllability of the transition distribution. However, this assumption is often violated when the dynamics evolves in a continuous space. Consequently, applying KL control to problems with continuous spaces requires some approximation, which leads to the lost of the optimality. To avoid such approximation, in this paper, we reformulate the KL control problem for continuous spaces so that it does not require unrealistic assumptions. The key difference between the original and reformulated KL control is that the former measures the control effort by KL divergence between controlled and uncontrolled transition distributions while the latter replaces the uncontrolled transition by a noise-driven transition. We show that the reformulated KL control admits efficient numerical algorithms like the original one without unreasonable assumptions. Specifically, the associated value function can be computed by using a Monte Carlo method based on its path integral representation.