Kullback-Leibler control for discrete-time nonlinear systems on continuous spaces
Paper and Code
Mar 24, 2022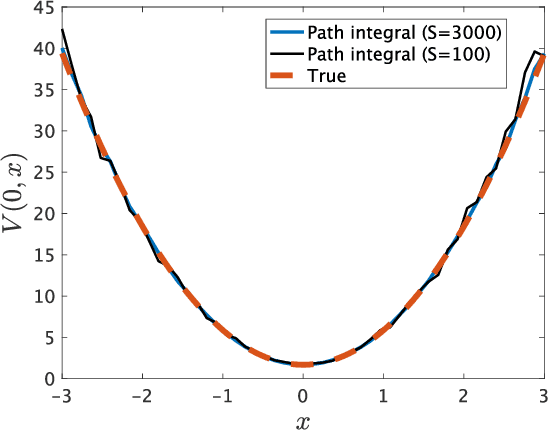
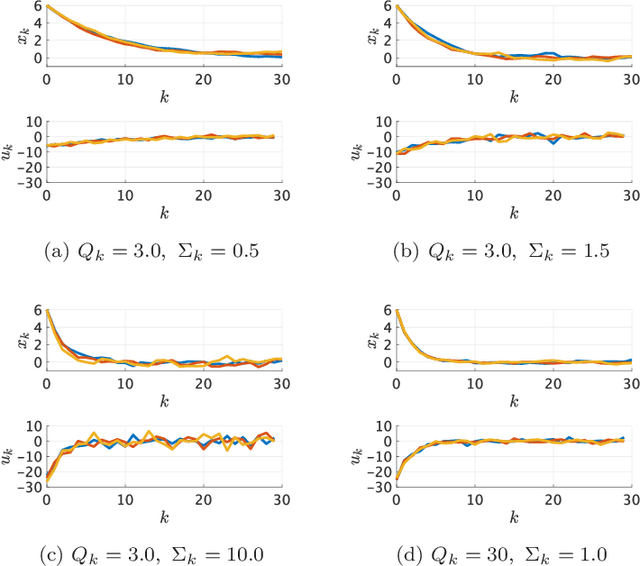
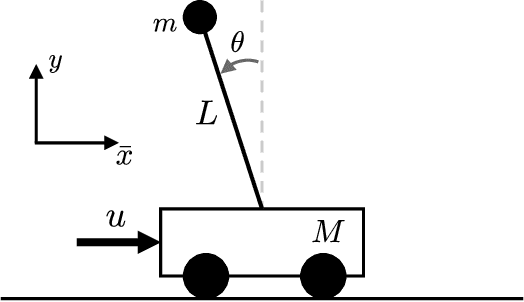
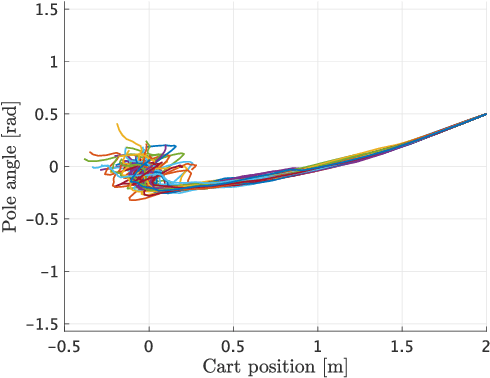
Kullback-Leibler (KL) control enables efficient numerical methods for nonlinear optimal control problems. The crucial assumption of KL control is the full controllability of the transition distribution. However, this assumption is often violated when the dynamics evolves in a continuous space. Consequently, applying KL control to problems with continuous spaces requires some approximation, which leads to the lost of the optimality. To avoid such approximation, in this paper, we reformulate the KL control problem for continuous spaces so that it does not require unrealistic assumptions. The key difference between the original and reformulated KL control is that the former measures the control effort by KL divergence between controlled and uncontrolled transition distributions while the latter replaces the uncontrolled transition by a noise-driven transition. We show that the reformulated KL control admits efficient numerical algorithms like the original one without unreasonable assumptions. Specifically, the associated value function can be computed by using a Monte Carlo method based on its path integral representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge