Kenji Kashima
Formation Shape Control using the Gromov-Wasserstein Metric
Mar 27, 2025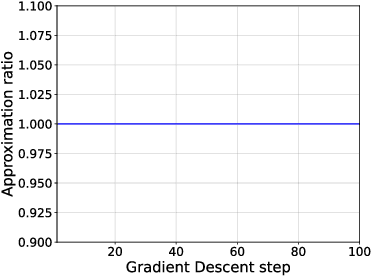
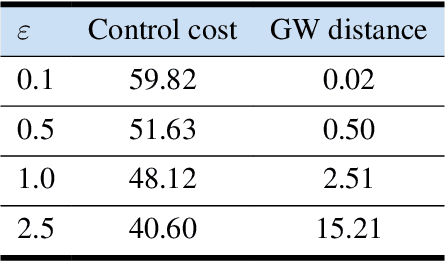
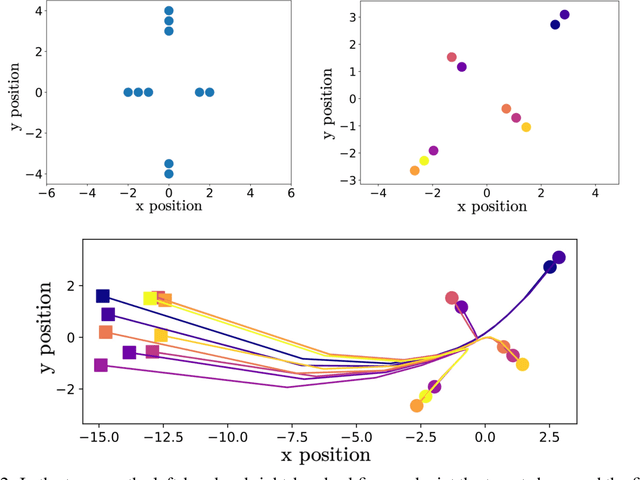
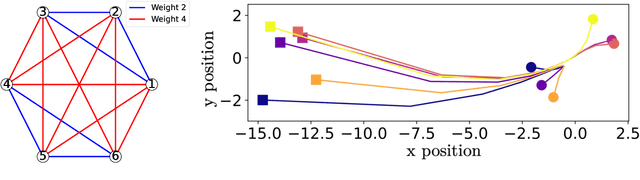
Abstract:This article introduces a formation shape control algorithm, in the optimal control framework, for steering an initial population of agents to a desired configuration via employing the Gromov-Wasserstein distance. The underlying dynamical system is assumed to be a constrained linear system and the objective function is a sum of quadratic control-dependent stage cost and a Gromov-Wasserstein terminal cost. The inclusion of the Gromov-Wasserstein cost transforms the resulting optimal control problem into a well-known NP-hard problem, making it both numerically demanding and difficult to solve with high accuracy. Towards that end, we employ a recent semi-definite relaxation-driven technique to tackle the Gromov-Wasserstein distance. A numerical example is provided to illustrate our results.
Risk-sensitive control as inference with Rényi divergence
Nov 04, 2024Abstract:This paper introduces the risk-sensitive control as inference (RCaI) that extends CaI by using R\'{e}nyi divergence variational inference. RCaI is shown to be equivalent to log-probability regularized risk-sensitive control, which is an extension of the maximum entropy (MaxEnt) control. We also prove that the risk-sensitive optimal policy can be obtained by solving a soft Bellman equation, which reveals several equivalences between RCaI, MaxEnt control, the optimal posterior for CaI, and linearly-solvable control. Moreover, based on RCaI, we derive the risk-sensitive reinforcement learning (RL) methods: the policy gradient and the soft actor-critic. As the risk-sensitivity parameter vanishes, we recover the risk-neutral CaI and RL, which means that RCaI is a unifying framework. Furthermore, we give another risk-sensitive generalization of the MaxEnt control using R\'{e}nyi entropy regularization. We show that in both of our extensions, the optimal policies have the same structure even though the derivations are very different.
Tsallis Entropy Regularization for Linearly Solvable MDP and Linear Quadratic Regulator
Mar 04, 2024Abstract:Shannon entropy regularization is widely adopted in optimal control due to its ability to promote exploration and enhance robustness, e.g., maximum entropy reinforcement learning known as Soft Actor-Critic. In this paper, Tsallis entropy, which is a one-parameter extension of Shannon entropy, is used for the regularization of linearly solvable MDP and linear quadratic regulators. We derive the solution for these problems and demonstrate its usefulness in balancing between exploration and sparsity of the obtained control law.
Imitation-regularized Optimal Transport on Networks: Provable Robustness and Application to Logistics Planning
Feb 28, 2024Abstract:Network systems form the foundation of modern society, playing a critical role in various applications. However, these systems are at significant risk of being adversely affected by unforeseen circumstances, such as disasters. Considering this, there is a pressing need for research to enhance the robustness of network systems. Recently, in reinforcement learning, the relationship between acquiring robustness and regularizing entropy has been identified. Additionally, imitation learning is used within this framework to reflect experts' behavior. However, there are no comprehensive studies on the use of a similar imitation framework for optimal transport on networks. Therefore, in this study, imitation-regularized optimal transport (I-OT) on networks was investigated. It encodes prior knowledge on the network by imitating a given prior distribution. The I-OT solution demonstrated robustness in terms of the cost defined on the network. Moreover, we applied the I-OT to a logistics planning problem using real data. We also examined the imitation and apriori risk information scenarios to demonstrate the usefulness and implications of the proposed method.
Learning Exactly Linearizable Deep Dynamics Models
Nov 30, 2023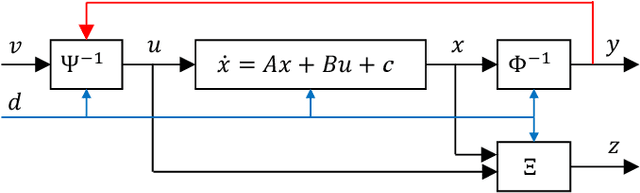
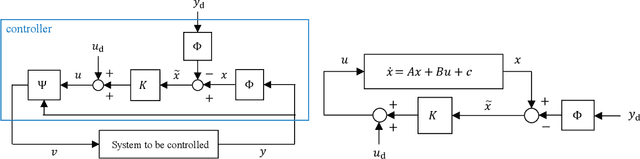
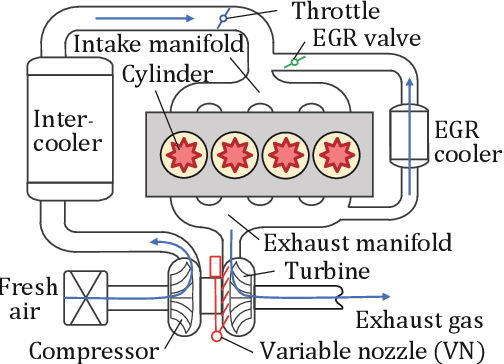
Abstract:Research on control using models based on machine-learning methods has now shifted to the practical engineering stage. Achieving high performance and theoretically guaranteeing the safety of the system is critical for such applications. In this paper, we propose a learning method for exactly linearizable dynamical models that can easily apply various control theories to ensure stability, reliability, etc., and to provide a high degree of freedom of expression. As an example, we present a design that combines simple linear control and control barrier functions. The proposed model is employed for the real-time control of an automotive engine, and the results demonstrate good predictive performance and stable control under constraints.
Resilience Evaluation of Entropy Regularized Logistic Networks with Probabilistic Cost
Dec 05, 2022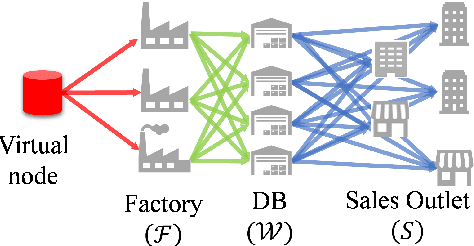
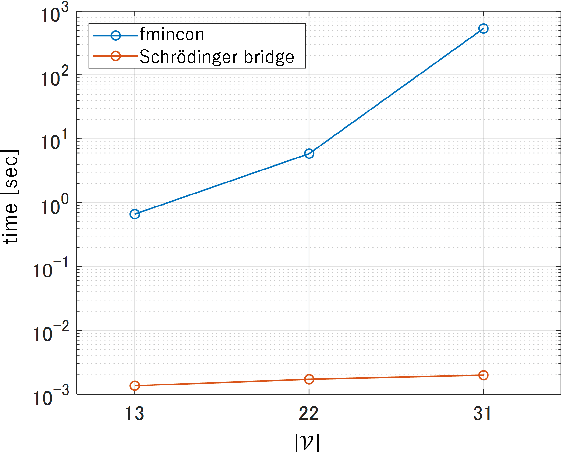
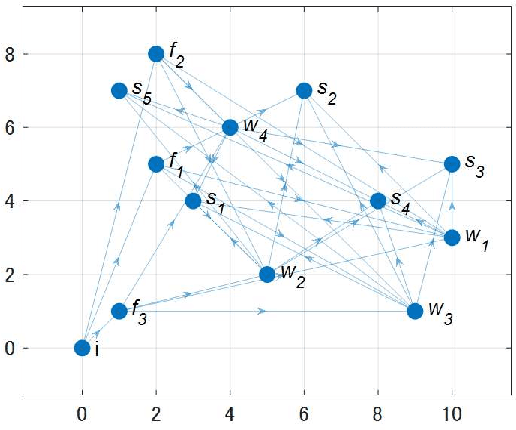
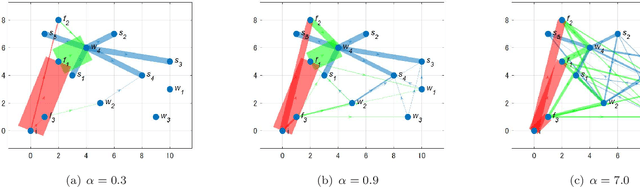
Abstract:The demand for resilient logistics networks has increased because of recent disasters. When we consider optimization problems, entropy regularization is a powerful tool for the diversification of a solution. In this study, we proposed a method for designing a resilient logistics network based on entropy regularization. Moreover, we proposed a method for analytical resilience criteria to reduce the ambiguity of resilience. First, we modeled the logistics network, including factories, distribution bases, and sales outlets in an efficient framework using entropy regularization. Next, we formulated a resilience criterion based on probabilistic cost and Kullback--Leibler divergence. Finally, our method was performed using a simple logistics network, and the resilience of the three logistics plans designed by entropy regularization was demonstrated.
Maximum entropy optimal density control of discrete-time linear systems and Schrödinger bridges
Apr 11, 2022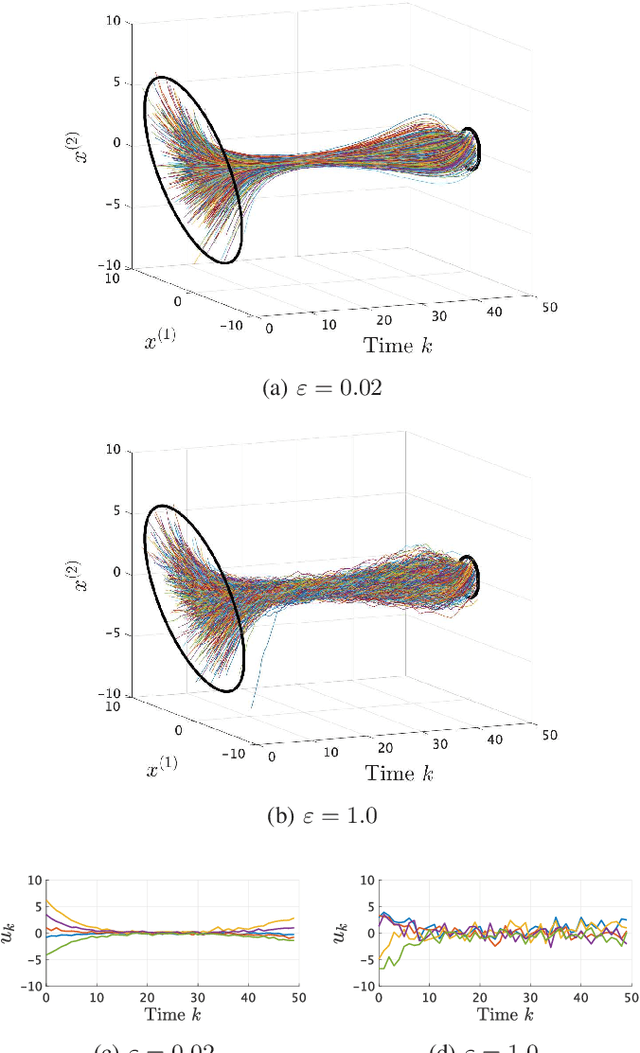
Abstract:We consider an entropy-regularized version of optimal density control of deterministic discrete-time linear systems. Entropy regularization, or a maximum entropy (MaxEnt) method for optimal control has attracted much attention especially in reinforcement learning due to its many advantages such as a natural exploration strategy. Despite the merits, high-entropy control policies introduce probabilistic uncertainty into systems, which severely limits the applicability of MaxEnt optimal control to safety-critical systems. To remedy this situation, we impose a Gaussian density constraint at a specified time on the MaxEnt optimal control to directly control state uncertainty. Specifically, we derive the explicit form of the MaxEnt optimal density control. In addition, we also consider the case where a density constraint is replaced by a fixed point constraint. Then, we characterize the associated state process as a pinned process, which is a generalization of the Brownian bridge to linear systems. Finally, we reveal that the MaxEnt optimal density control induces the so-called Schr\"odinger bridge associated to a discrete-time linear system.
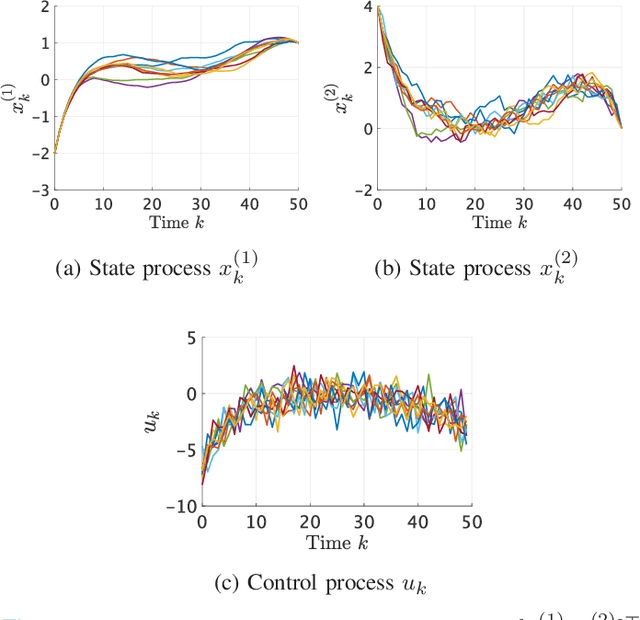
Kullback-Leibler control for discrete-time nonlinear systems on continuous spaces
Mar 24, 2022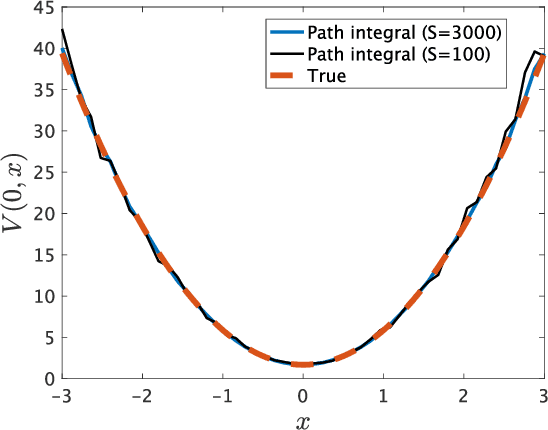
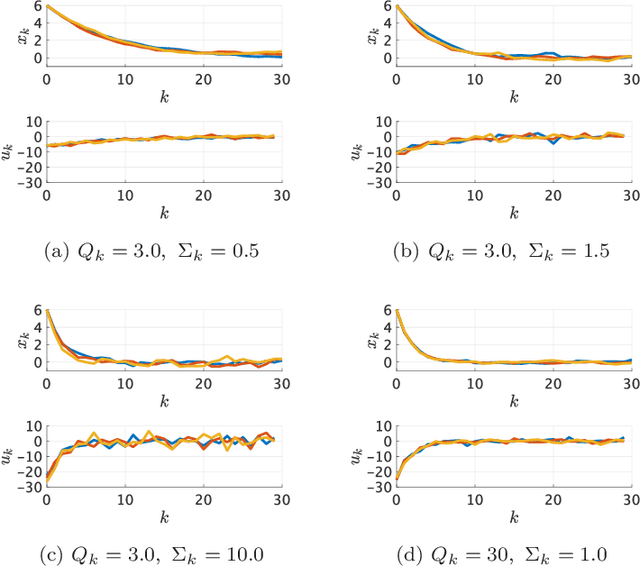
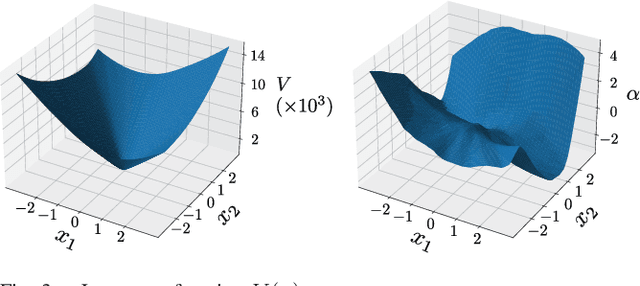
Abstract:Kullback-Leibler (KL) control enables efficient numerical methods for nonlinear optimal control problems. The crucial assumption of KL control is the full controllability of the transition distribution. However, this assumption is often violated when the dynamics evolves in a continuous space. Consequently, applying KL control to problems with continuous spaces requires some approximation, which leads to the lost of the optimality. To avoid such approximation, in this paper, we reformulate the KL control problem for continuous spaces so that it does not require unrealistic assumptions. The key difference between the original and reformulated KL control is that the former measures the control effort by KL divergence between controlled and uncontrolled transition distributions while the latter replaces the uncontrolled transition by a noise-driven transition. We show that the reformulated KL control admits efficient numerical algorithms like the original one without unreasonable assumptions. Specifically, the associated value function can be computed by using a Monte Carlo method based on its path integral representation.
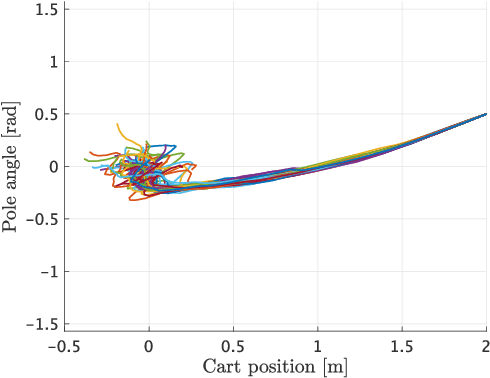
Learning Stabilizable Deep Dynamics Models
Mar 18, 2022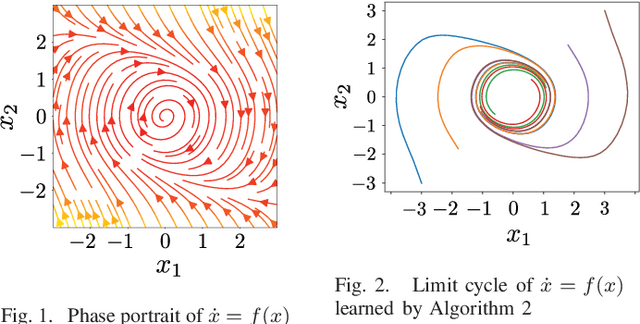
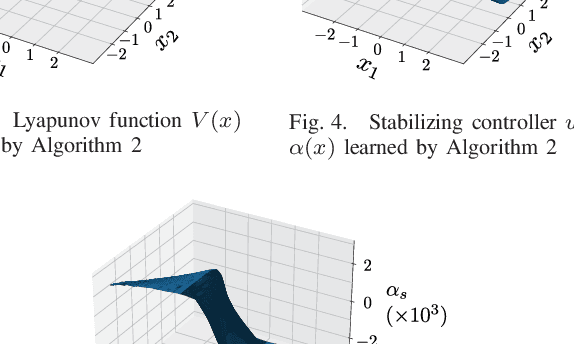
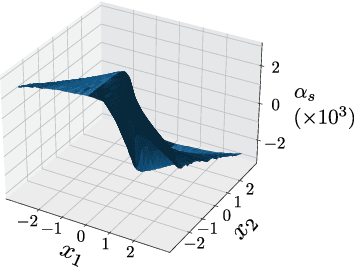
Abstract:When neural networks are used to model dynamics, properties such as stability of the dynamics are generally not guaranteed. In contrast, there is a recent method for learning the dynamics of autonomous systems that guarantees global exponential stability using neural networks. In this paper, we propose a new method for learning the dynamics of input-affine control systems. An important feature is that a stabilizing controller and control Lyapunov function of the learned model are obtained as well. Moreover, the proposed method can also be applied to solving Hamilton-Jacobi inequalities. The usefulness of the proposed method is examined through numerical examples.
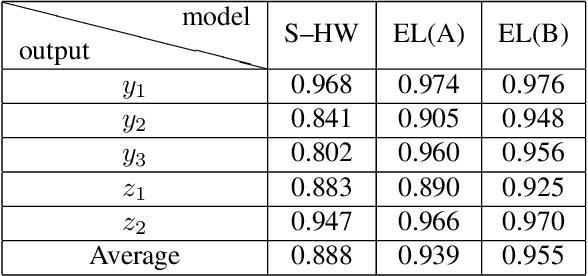
Structured Hammerstein-Wiener Model Learning for Model Predictive Control
Jul 09, 2021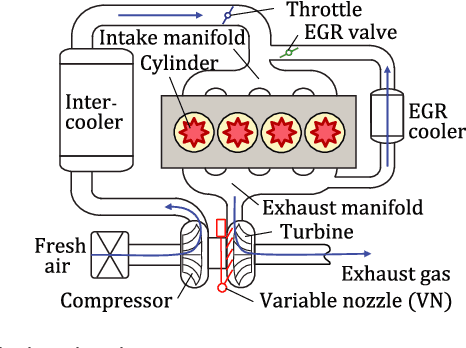

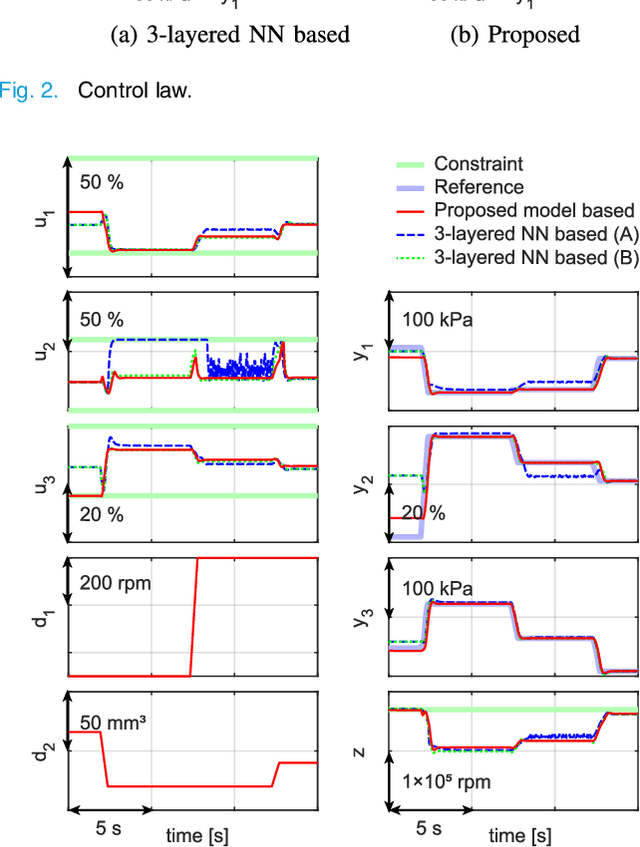
Abstract:This paper aims to improve the reliability of optimal control using models constructed by machine learning methods. Optimal control problems based on such models are generally non-convex and difficult to solve online. In this paper, we propose a model that combines the Hammerstein-Wiener model with input convex neural networks, which have recently been proposed in the field of machine learning. An important feature of the proposed model is that resulting optimal control problems are effectively solvable exploiting their convexity and partial linearity while retaining flexible modeling ability. The practical usefulness of the method is examined through its application to the modeling and control of an engine airpath system.
* 6 pages, 3 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge