Maximum entropy optimal density control of discrete-time linear systems and Schrödinger bridges

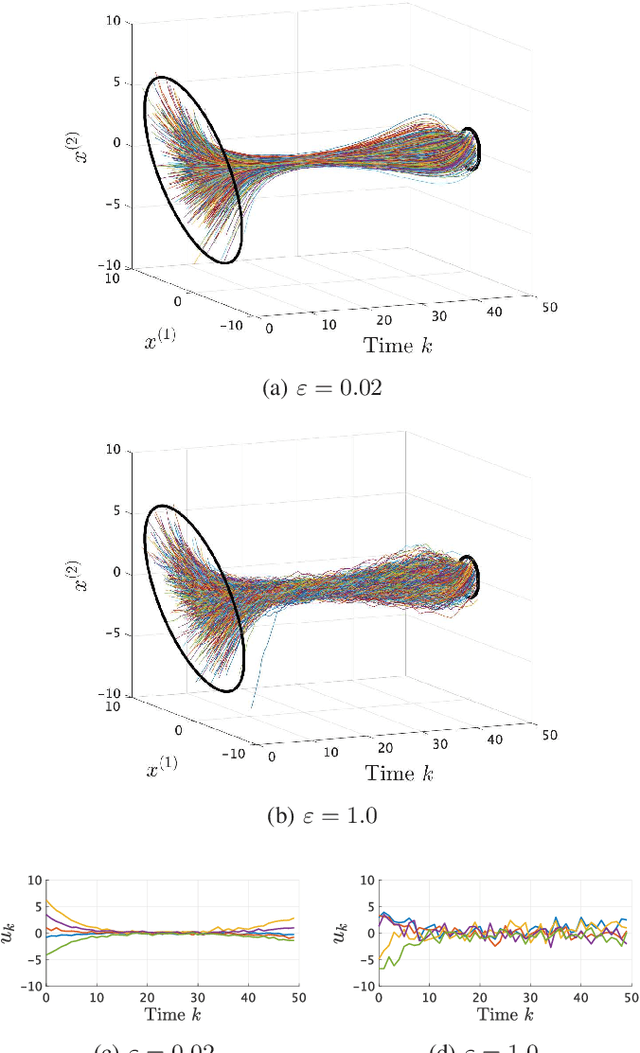
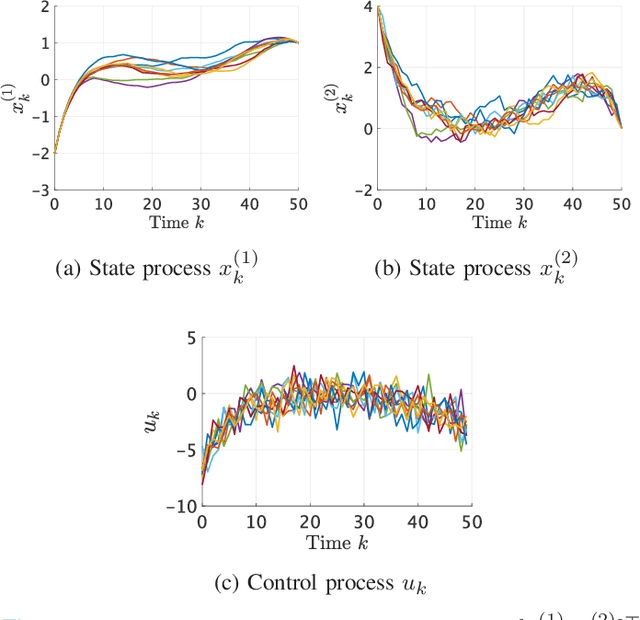
We consider an entropy-regularized version of optimal density control of deterministic discrete-time linear systems. Entropy regularization, or a maximum entropy (MaxEnt) method for optimal control has attracted much attention especially in reinforcement learning due to its many advantages such as a natural exploration strategy. Despite the merits, high-entropy control policies introduce probabilistic uncertainty into systems, which severely limits the applicability of MaxEnt optimal control to safety-critical systems. To remedy this situation, we impose a Gaussian density constraint at a specified time on the MaxEnt optimal control to directly control state uncertainty. Specifically, we derive the explicit form of the MaxEnt optimal density control. In addition, we also consider the case where a density constraint is replaced by a fixed point constraint. Then, we characterize the associated state process as a pinned process, which is a generalization of the Brownian bridge to linear systems. Finally, we reveal that the MaxEnt optimal density control induces the so-called Schr\"odinger bridge associated to a discrete-time linear system.