Tsallis Entropy Regularization for Linearly Solvable MDP and Linear Quadratic Regulator

Shannon entropy regularization is widely adopted in optimal control due to its ability to promote exploration and enhance robustness, e.g., maximum entropy reinforcement learning known as Soft Actor-Critic. In this paper, Tsallis entropy, which is a one-parameter extension of Shannon entropy, is used for the regularization of linearly solvable MDP and linear quadratic regulators. We derive the solution for these problems and demonstrate its usefulness in balancing between exploration and sparsity of the obtained control law.

Imitation-regularized Optimal Transport on Networks: Provable Robustness and Application to Logistics Planning

Network systems form the foundation of modern society, playing a critical role in various applications. However, these systems are at significant risk of being adversely affected by unforeseen circumstances, such as disasters. Considering this, there is a pressing need for research to enhance the robustness of network systems. Recently, in reinforcement learning, the relationship between acquiring robustness and regularizing entropy has been identified. Additionally, imitation learning is used within this framework to reflect experts' behavior. However, there are no comprehensive studies on the use of a similar imitation framework for optimal transport on networks. Therefore, in this study, imitation-regularized optimal transport (I-OT) on networks was investigated. It encodes prior knowledge on the network by imitating a given prior distribution. The I-OT solution demonstrated robustness in terms of the cost defined on the network. Moreover, we applied the I-OT to a logistics planning problem using real data. We also examined the imitation and apriori risk information scenarios to demonstrate the usefulness and implications of the proposed method.

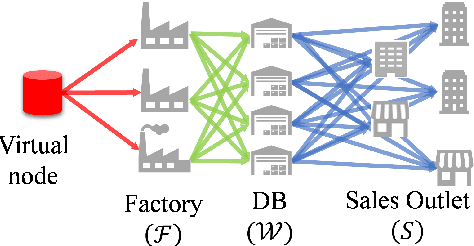
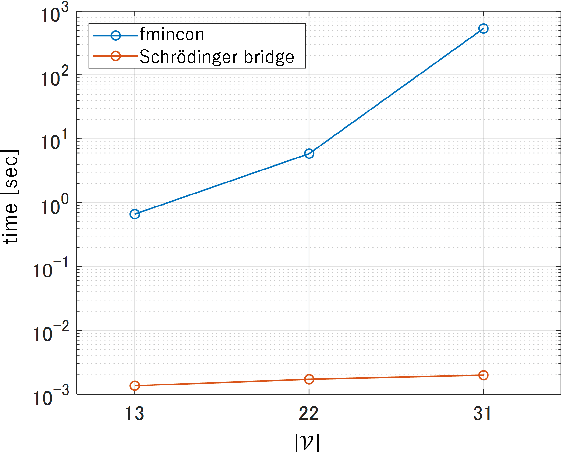
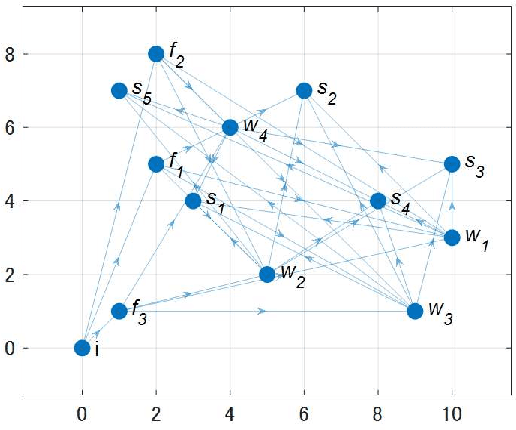
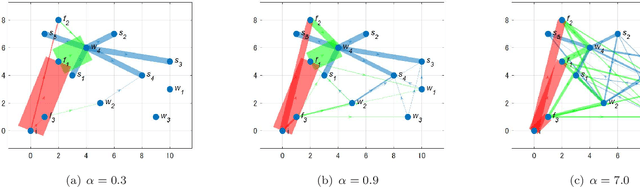
Resilience Evaluation of Entropy Regularized Logistic Networks with Probabilistic Cost

The demand for resilient logistics networks has increased because of recent disasters. When we consider optimization problems, entropy regularization is a powerful tool for the diversification of a solution. In this study, we proposed a method for designing a resilient logistics network based on entropy regularization. Moreover, we proposed a method for analytical resilience criteria to reduce the ambiguity of resilience. First, we modeled the logistics network, including factories, distribution bases, and sales outlets in an efficient framework using entropy regularization. Next, we formulated a resilience criterion based on probabilistic cost and Kullback--Leibler divergence. Finally, our method was performed using a simple logistics network, and the resilience of the three logistics plans designed by entropy regularization was demonstrated.