OT-DETECT: Optimal transport-driven attack detection in cyber-physical systems

This article presents an optimal-transport (OT)-driven, distributionally robust attack detection algorithm, OT-DETECT, for cyber-physical systems (CPS) modeled as partially observed linear stochastic systems. The underlying detection problem is formulated as a minmax optimization problem using 1-Wasserstein ambiguity sets constructed from observer residuals under both the nominal (attack-free) and attacked regimes. We show that the minmax detection problem can be reduced to a finite-dimensional linear program for computing the worst-case distribution (WCD). Off-support residuals are handled via a kernel-smoothed score function that drives a CUSUM procedure for sequential detection. We also establish a non-asymptotic tail bound on the false-positive error of the CUSUM statistic under the nominal (attack-free) condition, under mild assumptions. Numerical illustrations are provided to evaluate the robustness properties of OT-DETECT.

Robust maximum hands-off optimal control: existence, maximum principle, and $L^{0}$-$L^1$ equivalence

This work advances the maximum hands-off sparse control framework by developing a robust counterpart for constrained linear systems with parametric uncertainties. The resulting optimal control problem minimizes an $L^{0}$ objective subject to an uncountable, compact family of constraints, and is therefore a nonconvex, nonsmooth robust optimization problem. To address this, we replace the $L^{0}$ objective with its convex $L^{1}$ surrogate and, using a nonsmooth variant of the robust Pontryagin maximum principle, show that the $L^{0}$ and $L^{1}$ formulations have identical sets of optimal solutions -- we call this the robust hands-off principle. Building on this equivalence, we propose an algorithmic framework -- drawing on numerically viable techniques from the semi-infinite robust optimization literature -- to solve the resulting problems. An illustrative example is provided to demonstrate the effectiveness of the approach.

Formation Shape Control using the Gromov-Wasserstein Metric

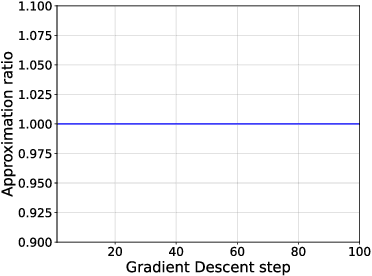
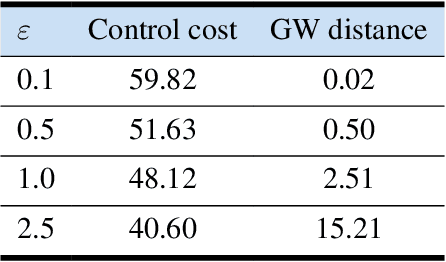
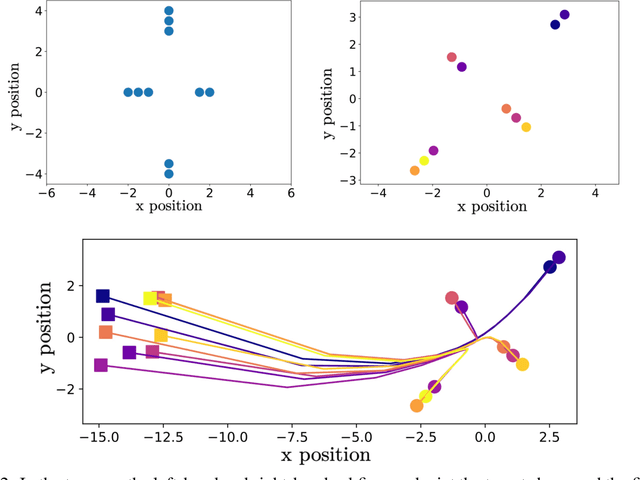
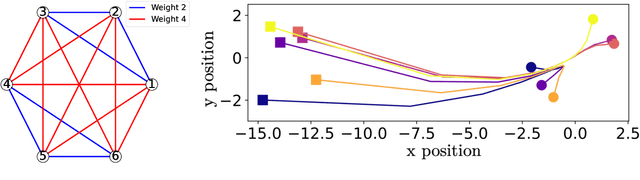
This article introduces a formation shape control algorithm, in the optimal control framework, for steering an initial population of agents to a desired configuration via employing the Gromov-Wasserstein distance. The underlying dynamical system is assumed to be a constrained linear system and the objective function is a sum of quadratic control-dependent stage cost and a Gromov-Wasserstein terminal cost. The inclusion of the Gromov-Wasserstein cost transforms the resulting optimal control problem into a well-known NP-hard problem, making it both numerically demanding and difficult to solve with high accuracy. Towards that end, we employ a recent semi-definite relaxation-driven technique to tackle the Gromov-Wasserstein distance. A numerical example is provided to illustrate our results.