Online Inverse Linear Optimization: Improved Regret Bound, Robustness to Suboptimality, and Toward Tight Regret Analysis

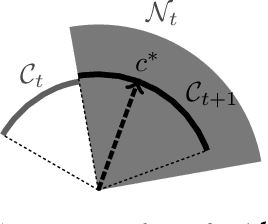
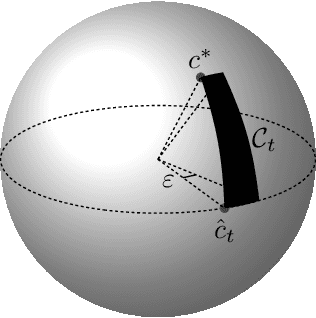
We study an online learning problem where, over $T$ rounds, a learner observes both time-varying sets of feasible actions and an agent's optimal actions, selected by solving linear optimization over the feasible actions. The learner sequentially makes predictions of the agent's underlying linear objective function, and their quality is measured by the regret, the cumulative gap between optimal objective values and those achieved by following the learner's predictions. A seminal work by B\"armann et al. (ICML 2017) showed that online learning methods can be applied to this problem to achieve regret bounds of $O(\sqrt{T})$. Recently, Besbes et al. (COLT 2021, Oper. Res. 2023) significantly improved the result by achieving an $O(n^4\ln T)$ regret bound, where $n$ is the dimension of the ambient space of objective vectors. Their method, based on the ellipsoid method, runs in polynomial time but is inefficient for large $n$ and $T$. In this paper, we obtain an $O(n\ln T)$ regret bound, improving upon the previous bound of $O(n^4\ln T)$ by a factor of $n^3$. Our method is simple and efficient: we apply the online Newton step (ONS) to appropriate exp-concave loss functions. Moreover, for the case where the agent's actions are possibly suboptimal, we establish an $O(n\ln T+\sqrt{\Delta_Tn\ln T})$ regret bound, where $\Delta_T$ is the cumulative suboptimality of the agent's actions. This bound is achieved by using MetaGrad, which runs ONS with $\Theta(\ln T)$ different learning rates in parallel. We also provide a simple instance that implies an $\Omega(n)$ lower bound, showing that our $O(n\ln T)$ bound is tight up to an $O(\ln T)$ factor. This gives rise to a natural question: can the $O(\ln T)$ factor in the upper bound be removed? For the special case of $n=2$, we show that an $O(1)$ regret bound is possible, while we delineate challenges in extending this result to higher dimensions.

No-Regret M${}^{ atural}$-Concave Function Maximization: Stochastic Bandit Algorithms and NP-Hardness of Adversarial Full-Information Setting

M${}^{\natural}$-concave functions, a.k.a. gross substitute valuation functions, play a fundamental role in many fields, including discrete mathematics and economics. In practice, perfect knowledge of M${}^{\natural}$-concave functions is often unavailable a priori, and we can optimize them only interactively based on some feedback. Motivated by such situations, we study online M${}^{\natural}$-concave function maximization problems, which are interactive versions of the problem studied by Murota and Shioura (1999). For the stochastic bandit setting, we present $O(T^{-1/2})$-simple regret and $O(T^{2/3})$-regret algorithms under $T$ times access to unbiased noisy value oracles of M${}^{\natural}$-concave functions. A key to proving these results is the robustness of the greedy algorithm to local errors in M${}^{\natural}$-concave function maximization, which is one of our main technical results. While we obtain those positive results for the stochastic setting, another main result of our work is an impossibility in the adversarial setting. We prove that, even with full-information feedback, no algorithms that run in polynomial time per round can achieve $O(T^{1-c})$ regret for any constant $c > 0$ unless $\mathsf{P} = \mathsf{NP}$. Our proof is based on a reduction from the matroid intersection problem for three matroids, which would be a novel idea in the context of online learning.

Online Structured Prediction with Fenchel--Young Losses and Improved Surrogate Regret for Online Multiclass Classification with Logistic Loss

This paper studies online structured prediction with full-information feedback. For online multiclass classification, van der Hoeven (2020) has obtained surrogate regret bounds independent of the time horizon, or \emph{finite}, by introducing an elegant \emph{exploit-the-surrogate-gap} framework. However, this framework has been limited to multiclass classification primarily because it relies on a classification-specific procedure for converting estimated scores to outputs. We extend the exploit-the-surrogate-gap framework to online structured prediction with \emph{Fenchel--Young losses}, a large family of surrogate losses including the logistic loss for multiclass classification, obtaining finite surrogate regret bounds in various structured prediction problems. To this end, we propose and analyze \emph{randomized decoding}, which converts estimated scores to general structured outputs. Moreover, by applying our decoding to online multiclass classification with the logistic loss, we obtain a surrogate regret bound of $O(B^2)$, where $B$ is the $\ell_2$-diameter of the domain. This bound is tight up to logarithmic factors and improves the previous bound of $O(dB^2)$ due to van der Hoeven (2020) by a factor of $d$, the number of classes.

Data-Driven Projection for Reducing Dimensionality of Linear Programs: Generalization Bound and Learning Methods

This paper studies a simple data-driven approach to high-dimensional linear programs (LPs). Given data of past $n$-dimensional LPs, we learn an $n\times k$ \textit{projection matrix} ($n > k$), which reduces the dimensionality from $n$ to $k$. Then, we address future LP instances by solving $k$-dimensional LPs and recovering $n$-dimensional solutions by multiplying the projection matrix. This idea is compatible with any user-preferred LP solvers, hence a versatile approach to faster LP solving. One natural question is: how much data is sufficient to ensure the recovered solutions' quality? We address this question based on the idea of \textit{data-driven algorithm design}, which relates the amount of data sufficient for generalization guarantees to the \textit{pseudo-dimension} of performance metrics. We present an $\tilde{\mathrm{O}}(nk^2)$ upper bound on the pseudo-dimension ($\tilde{\mathrm{O}}$ compresses logarithmic factors) and complement it by an $\Omega(nk)$ lower bound, hence tight up to an $\tilde{\mathrm{O}}(k)$ factor. On the practical side, we study two natural methods for learning projection matrices: PCA- and gradient-based methods. While the former is simple and efficient, the latter sometimes leads to better solution quality. Experiments confirm that learned projection matrices are beneficial for reducing the time for solving LPs while maintaining high solution quality.

Faster Discrete Convex Function Minimization with Predictions: The M-Convex Case

Recent years have seen a growing interest in accelerating optimization algorithms with machine-learned predictions. Sakaue and Oki (NeurIPS 2022) have developed a general framework that warm-starts the L-convex function minimization method with predictions, revealing the idea's usefulness for various discrete optimization problems. In this paper, we present a framework for using predictions to accelerate M-convex function minimization, thus complementing previous research and extending the range of discrete optimization algorithms that can benefit from predictions. Our framework is particularly effective for an important subclass called laminar convex minimization, which appears in many operations research applications. Our methods can improve time complexity bounds upon the best worst-case results by using predictions and even have potential to go beyond a lower-bound result.

Rethinking Warm-Starts with Predictions: Learning Predictions Close to Sets of Optimal Solutions for Faster $\text{L}$-/$\text{L}^ atural$-Convex Function Minimization

An emerging line of work has shown that machine-learned predictions are useful to warm-start algorithms for discrete optimization problems, such as bipartite matching. Previous studies have shown time complexity bounds proportional to some distance between a prediction and an optimal solution, which we can approximately minimize by learning predictions from past optimal solutions. However, such guarantees may not be meaningful when multiple optimal solutions exist. Indeed, the dual problem of bipartite matching and, more generally, $\text{L}$-/$\text{L}^\natural$-convex function minimization have arbitrarily many optimal solutions, making such prediction-dependent bounds arbitrarily large. To resolve this theoretically critical issue, we present a new warm-start-with-prediction framework for $\text{L}$-/$\text{L}^\natural$-convex function minimization. Our framework offers time complexity bounds proportional to the distance between a prediction and the set of all optimal solutions. The main technical difficulty lies in learning predictions that are provably close to sets of all optimal solutions, for which we present an online-gradient-descent-based method. We thus give the first polynomial-time learnability of predictions that can provably warm-start algorithms regardless of multiple optimal solutions.

Improved Generalization Bound and Learning of Sparsity Patterns for Data-Driven Low-Rank Approximation

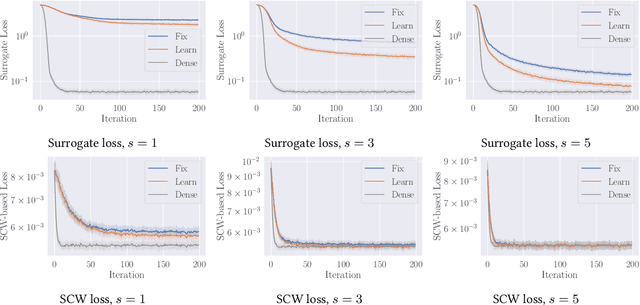
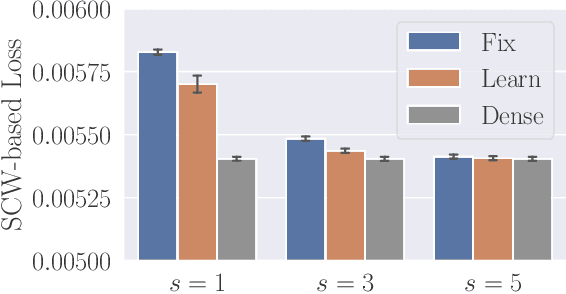
Learning sketching matrices for fast and accurate low-rank approximation (LRA) has gained increasing attention. Recently, Bartlett, Indyk, and Wagner (COLT 2022) presented a generalization bound for the learning-based LRA. Specifically, for rank-$k$ approximation using an $m \times n$ learned sketching matrix with $s$ non-zeros in each column, they proved an $\tilde{\mathrm{O}}(nsm)$ bound on the \emph{fat shattering dimension} ($\tilde{\mathrm{O}}$ hides logarithmic factors). We build on their work and make two contributions. 1. We present a better $\tilde{\mathrm{O}}(nsk)$ bound ($k \le m$). En route to obtaining the bound, we give a low-complexity \emph{Goldberg--Jerrum algorithm} for computing pseudo-inverse matrices, which would be of independent interest. 2. We alleviate an assumption of the previous study that the sparsity pattern of sketching matrices is fixed. We prove that learning positions of non-zeros increases the fat shattering dimension only by ${\mathrm{O}}(ns\log n)$. Also, experiments confirm the practical benefit of learning sparsity patterns.

Lazy and Fast Greedy MAP Inference for Determinantal Point Process

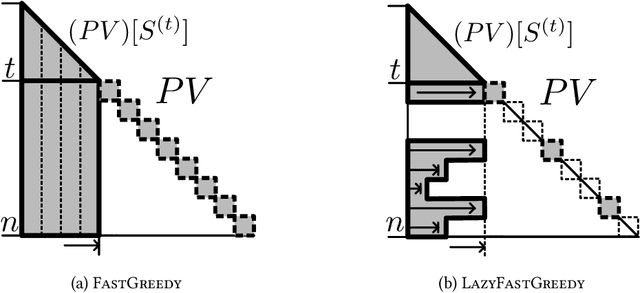
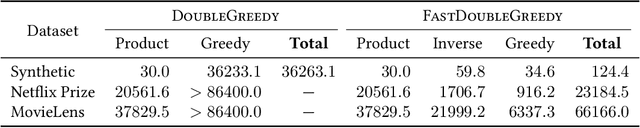
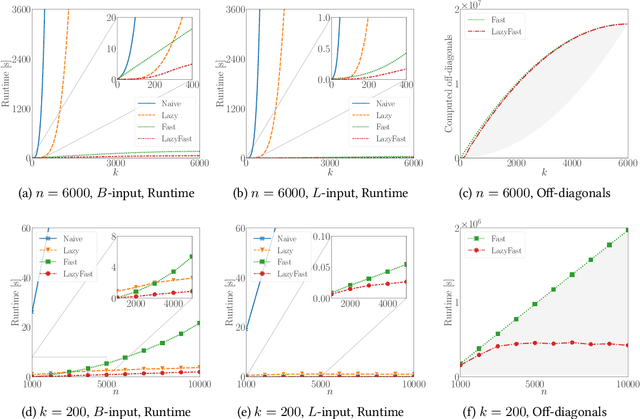
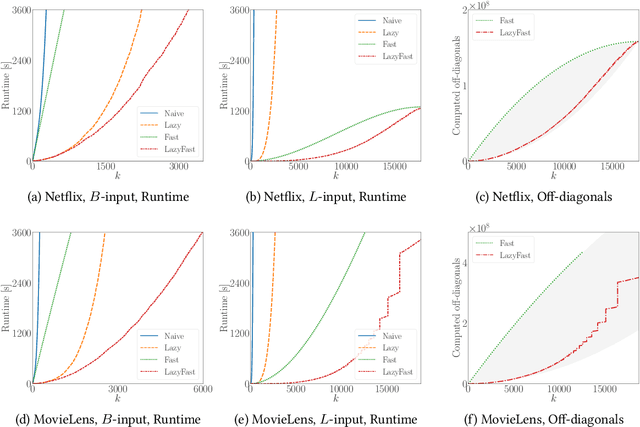
The maximum a posteriori (MAP) inference for determinantal point processes (DPPs) is crucial for selecting diverse items in many machine learning applications. Although DPP MAP inference is NP-hard, the greedy algorithm often finds high-quality solutions, and many researchers have studied its efficient implementation. One classical and practical method is the lazy greedy algorithm, which is applicable to general submodular function maximization, while a recent fast greedy algorithm based on the Cholesky factorization is more efficient for DPP MAP inference. This paper presents how to combine the ideas of "lazy" and "fast", which have been considered incompatible in the literature. Our lazy and fast greedy algorithm achieves almost the same time complexity as the current best one and runs faster in practice. The idea of "lazy + fast" is extendable to other greedy-type algorithms. We also give a fast version of the double greedy algorithm for unconstrained DPP MAP inference. Experiments validate the effectiveness of our acceleration ideas.

Sample Complexity of Learning Heuristic Functions for Greedy-Best-First and A* Search

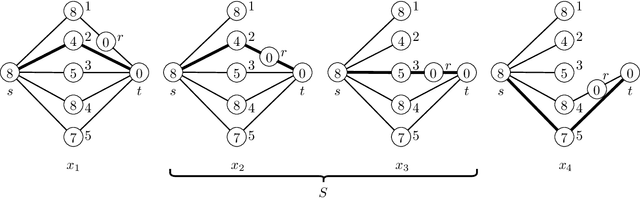
Greedy best-first search (GBFS) and A* search (A*) are popular algorithms for path-finding on large graphs. Both use so-called heuristic functions, which estimate how close a vertex is to the goal. While heuristic functions have been handcrafted using domain knowledge, recent studies demonstrate that learning heuristic functions from data is effective in many applications. Motivated by this emerging approach, we study the sample complexity of learning heuristic functions for GBFS and A*. We build on a recent framework called \textit{data-driven algorithm design} and evaluate the \textit{pseudo-dimension} of a class of utility functions that measure the performance of parameterized algorithms. Assuming that a vertex set of size $n$ is fixed, we present $\mathrm{O}(n\lg n)$ and $\mathrm{O}(n^2\lg n)$ upper bounds on the pseudo-dimensions for GBFS and A*, respectively, parameterized by heuristic function values. The upper bound for A* can be improved to $\mathrm{O}(n^2\lg d)$ if every vertex has a degree of at most $d$ and to $\mathrm{O}(n \lg n)$ if edge weights are integers bounded by $\mathrm{poly}(n)$. We also give $\Omega(n)$ lower bounds for GBFS and A*, which imply that our bounds for GBFS and A* under the integer-weight condition are tight up to a $\lg n$ factor. Finally, we discuss a case where the performance of A* is measured by the suboptimality and show that we can sometimes obtain a better guarantee by combining a parameter-dependent worst-case bound with a sample complexity bound.

Discrete-Convex-Analysis-Based Framework for Warm-Starting Algorithms with Predictions

Augmenting algorithms with learned predictions is a promising approach for going beyond worst-case bounds. Dinitz, Im, Lavastida, Moseley, and Vassilvitskii~(2021) have demonstrated that a warm start with learned dual solutions can improve the time complexity of the Hungarian method for weighted perfect bipartite matching. We extend and improve their framework in a principled manner via \textit{discrete convex analysis} (DCA), a discrete analog of convex analysis. We show the usefulness of our DCA-based framework by applying it to weighted perfect bipartite matching, weighted matroid intersection, and discrete energy minimization for computer vision. Our DCA-based framework yields time complexity bounds that depend on the $\ell_\infty$-distance from a predicted solution to an optimal solution, which has two advantages relative to the previous $\ell_1$-distance-dependent bounds: time complexity bounds are smaller, and learning of predictions is more sample efficient. We also discuss whether to learn primal or dual solutions from the DCA perspective.