Bayes correlated equilibria and no-regret dynamics

This paper explores equilibrium concepts for Bayesian games, which are fundamental models of games with incomplete information. We aim at three desirable properties of equilibria. First, equilibria can be naturally realized by introducing a mediator into games. Second, an equilibrium can be computed efficiently in a distributed fashion. Third, any equilibrium in that class approximately maximizes social welfare, as measured by the price of anarchy, for a broad class of games. These three properties allow players to compute an equilibrium and realize it via a mediator, thereby settling into a stable state with approximately optimal social welfare. Our main result is the existence of an equilibrium concept that satisfies these three properties. Toward this goal, we characterize various (non-equivalent) extensions of correlated equilibria, collectively known as Bayes correlated equilibria. In particular, we focus on communication equilibria (also known as coordination mechanisms), which can be realized by a mediator who gathers each player's private information and then sends correlated recommendations to the players. We show that if each player minimizes a variant of regret called untruthful swap regret in repeated play of Bayesian games, the empirical distribution of these dynamics converges to a communication equilibrium. We present an efficient algorithm for minimizing untruthful swap regret with a sublinear upper bound, which we prove to be tight up to a multiplicative constant. As a result, by simulating the dynamics with our algorithm, we can efficiently compute an approximate communication equilibrium. Furthermore, we extend existing lower bounds on the price of anarchy based on the smoothness arguments from Bayes Nash equilibria to equilibria obtained by the proposed dynamics.

Lazy and Fast Greedy MAP Inference for Determinantal Point Process

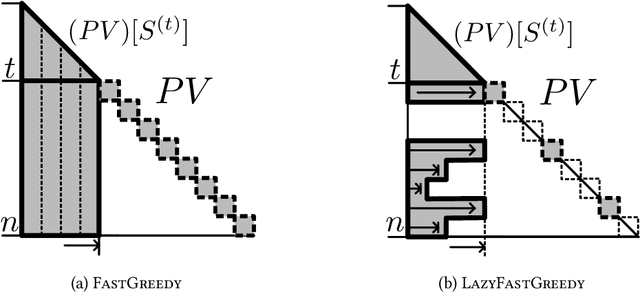
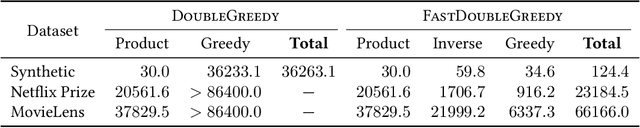
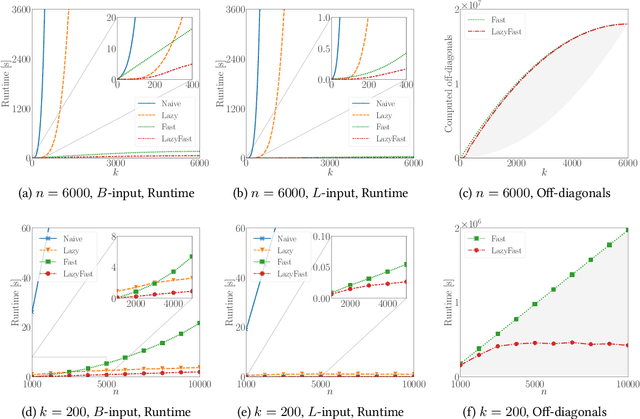
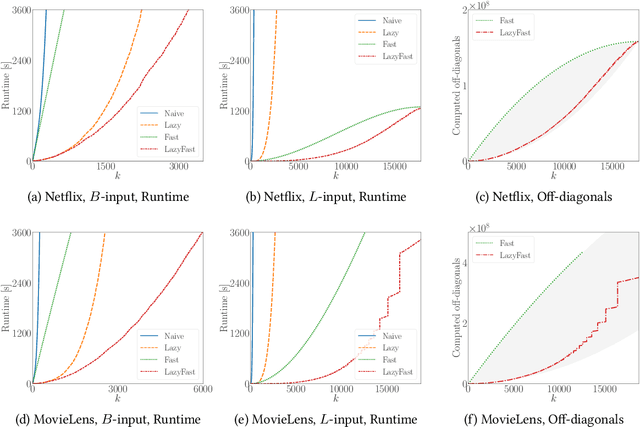
The maximum a posteriori (MAP) inference for determinantal point processes (DPPs) is crucial for selecting diverse items in many machine learning applications. Although DPP MAP inference is NP-hard, the greedy algorithm often finds high-quality solutions, and many researchers have studied its efficient implementation. One classical and practical method is the lazy greedy algorithm, which is applicable to general submodular function maximization, while a recent fast greedy algorithm based on the Cholesky factorization is more efficient for DPP MAP inference. This paper presents how to combine the ideas of "lazy" and "fast", which have been considered incompatible in the literature. Our lazy and fast greedy algorithm achieves almost the same time complexity as the current best one and runs faster in practice. The idea of "lazy + fast" is extendable to other greedy-type algorithms. We also give a fast version of the double greedy algorithm for unconstrained DPP MAP inference. Experiments validate the effectiveness of our acceleration ideas.

Approximation Guarantees of Local Search Algorithms via Localizability of Set Functions

This paper proposes a new framework for providing approximation guarantees of local search algorithms. Local search is a basic algorithm design technique and is widely used for various combinatorial optimization problems. To analyze local search algorithms for set function maximization, we propose a new notion called localizability of set functions, which measures how effective local improvement is. Moreover, we provide approximation guarantees of standard local search algorithms under various combinatorial constraints in terms of localizability. The main application of our framework is sparse optimization, for which we show that restricted strong concavity and restricted smoothness of the objective function imply localizability, and further develop accelerated versions of local search algorithms. We conduct experiments in sparse regression and structure learning of graphical models to confirm the practical efficiency of the proposed local search algorithms.

Beyond Adaptive Submodularity: Approximation Guarantees of Greedy Policy with Adaptive Submodularity Ratio

We propose a new concept named adaptive submodularity ratio to study the greedy policy for sequential decision making. While the greedy policy is known to perform well for a wide variety of adaptive stochastic optimization problems in practice, its theoretical properties have been analyzed only for a limited class of problems. We narrow the gap between theory and practice by using adaptive submodularity ratio, which enables us to prove approximation guarantees of the greedy policy for a substantially wider class of problems. Examples of newly analyzed problems include important applications such as adaptive influence maximization and adaptive feature selection. Our adaptive submodularity ratio also provides bounds of adaptivity gaps. Experiments confirm that the greedy policy performs well with the applications being considered compared to standard heuristics.

Fast greedy algorithms for dictionary selection with generalized sparsity constraints

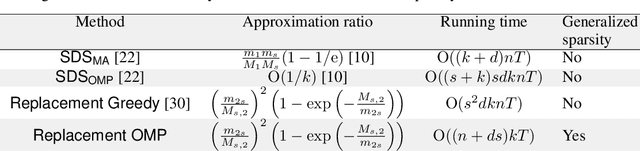
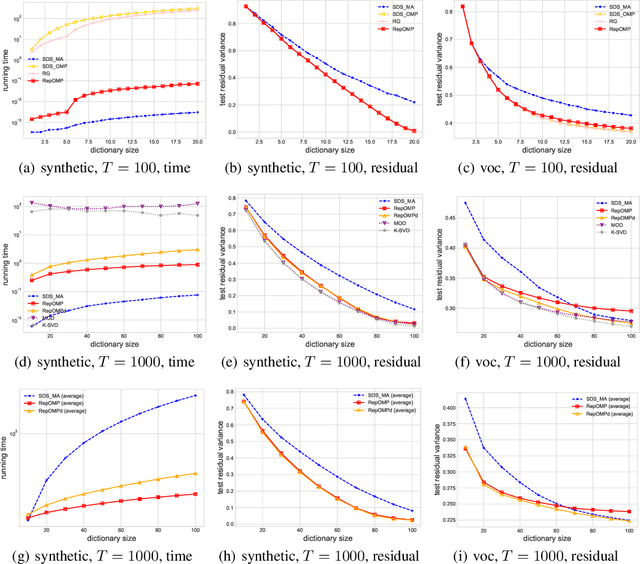
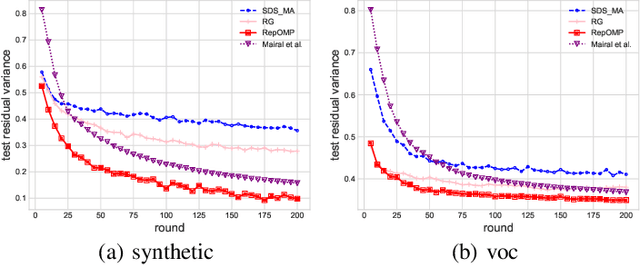
In dictionary selection, several atoms are selected from finite candidates that successfully approximate given data points in the sparse representation. We propose a novel efficient greedy algorithm for dictionary selection. Not only does our algorithm work much faster than the known methods, but it can also handle more complex sparsity constraints, such as average sparsity. Using numerical experiments, we show that our algorithm outperforms the known methods for dictionary selection, achieving competitive performances with dictionary learning algorithms in a smaller running time.