Optimal algorithms for group distributionally robust optimization and beyond

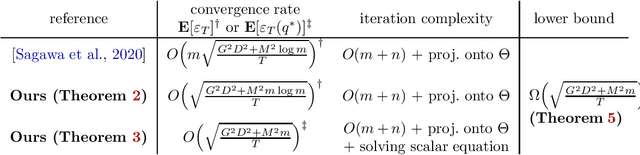
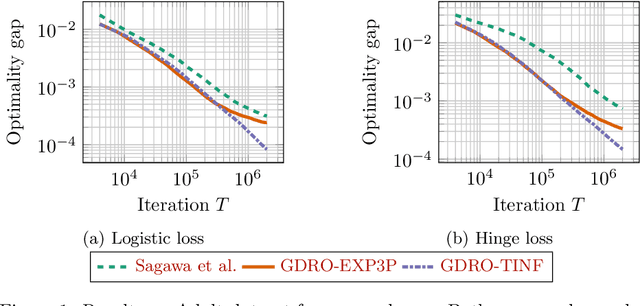
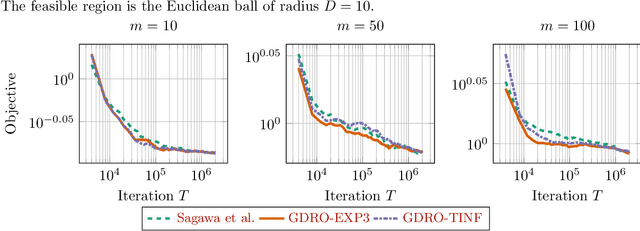
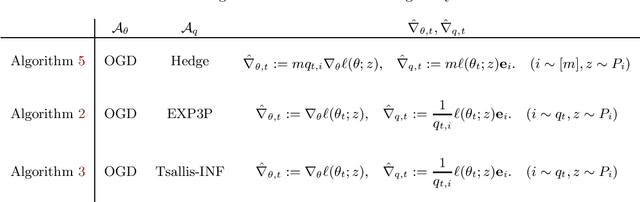
Distributionally robust optimization (DRO) can improve the robustness and fairness of learning methods. In this paper, we devise stochastic algorithms for a class of DRO problems including group DRO, subpopulation fairness, and empirical conditional value at risk (CVaR) optimization. Our new algorithms achieve faster convergence rates than existing algorithms for multiple DRO settings. We also provide a new information-theoretic lower bound that implies our bounds are tight for group DRO. Empirically, too, our algorithms outperform known methods

Statistical Learning with Conditional Value at Risk

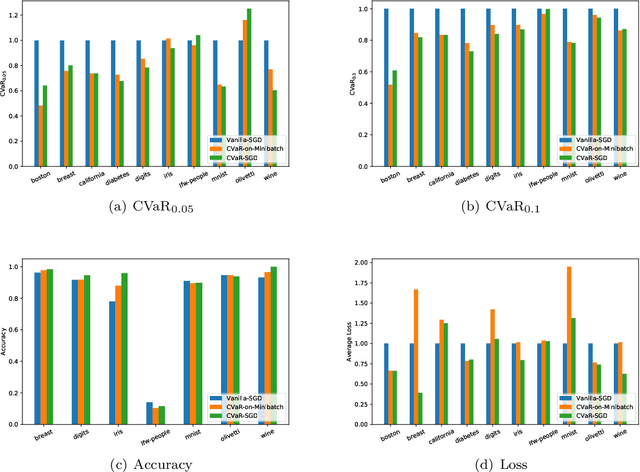
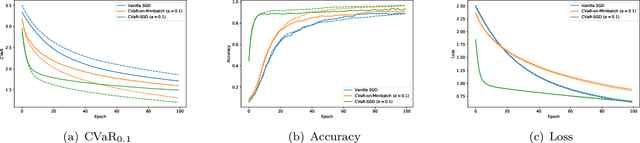
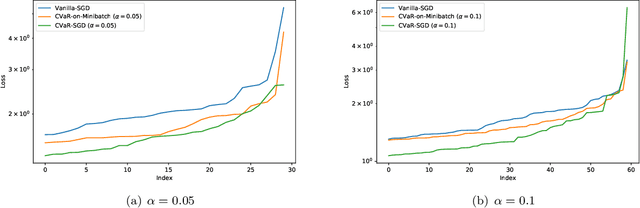
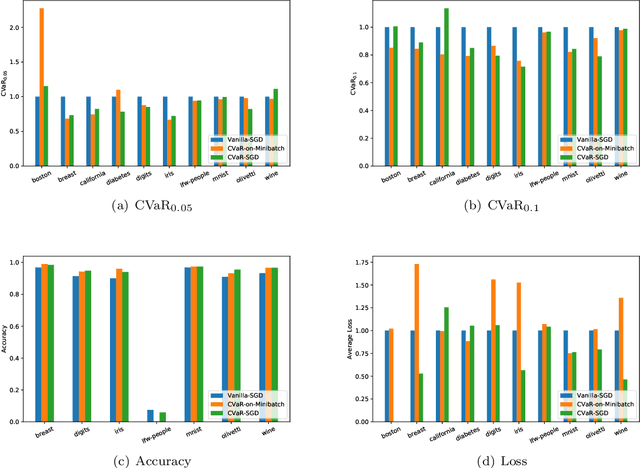
We propose a risk-averse statistical learning framework wherein the performance of a learning algorithm is evaluated by the conditional value-at-risk (CVaR) of losses rather than the expected loss. We devise algorithms based on stochastic gradient descent for this framework. While existing studies of CVaR optimization require direct access to the underlying distribution, our algorithms make a weaker assumption that only i.i.d.\ samples are given. For convex and Lipschitz loss functions, we show that our algorithm has $O(1/\sqrt{n})$-convergence to the optimal CVaR, where $n$ is the number of samples. For nonconvex and smooth loss functions, we show a generalization bound on CVaR. By conducting numerical experiments on various machine learning tasks, we demonstrate that our algorithms effectively minimize CVaR compared with other baseline algorithms.

Fast greedy algorithms for dictionary selection with generalized sparsity constraints

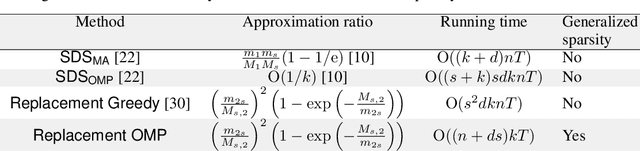
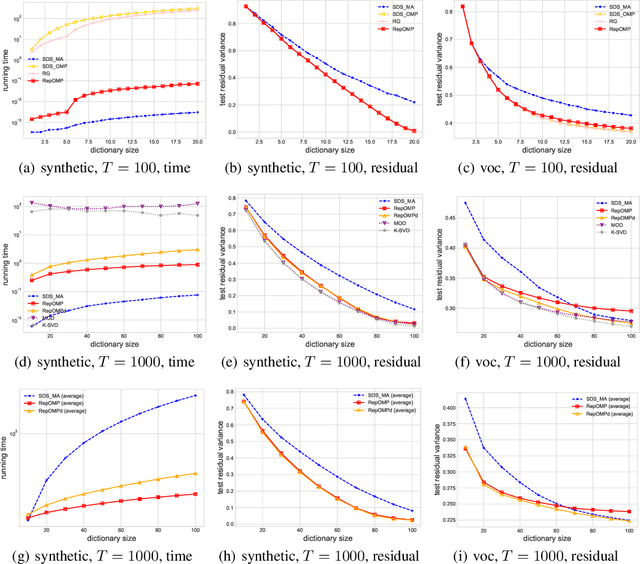
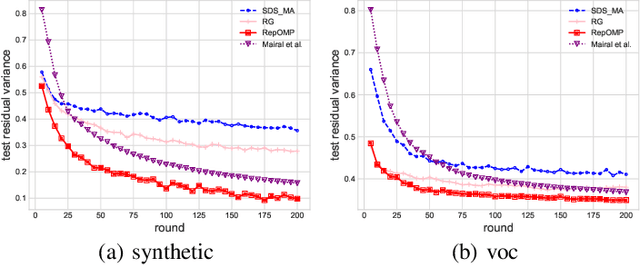
In dictionary selection, several atoms are selected from finite candidates that successfully approximate given data points in the sparse representation. We propose a novel efficient greedy algorithm for dictionary selection. Not only does our algorithm work much faster than the known methods, but it can also handle more complex sparsity constraints, such as average sparsity. Using numerical experiments, we show that our algorithm outperforms the known methods for dictionary selection, achieving competitive performances with dictionary learning algorithms in a smaller running time.

Maximally Invariant Data Perturbation as Explanation

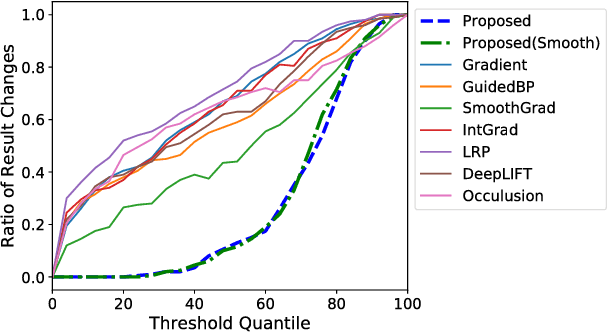
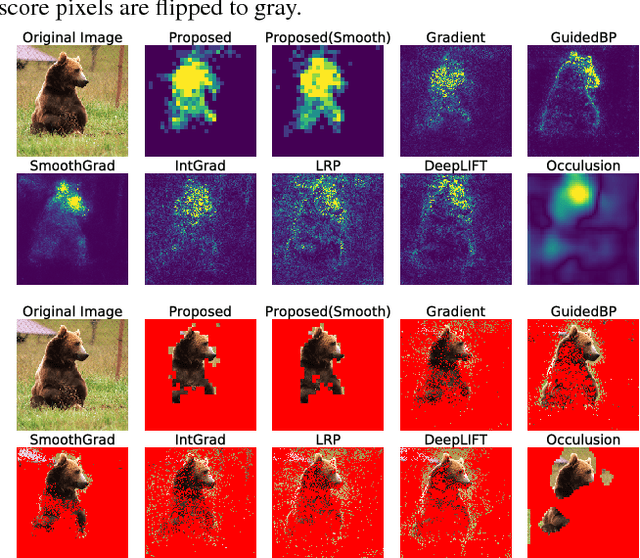
While several feature scoring methods are proposed to explain the output of complex machine learning models, most of them lack formal mathematical definitions. In this study, we propose a novel definition of the feature score using the maximally invariant data perturbation, which is inspired from the idea of adversarial example. In adversarial example, one seeks the smallest data perturbation that changes the model's output. In our proposed approach, we consider the opposite: we seek the maximally invariant data perturbation that does not change the model's output. In this way, we can identify important input features as the ones with small allowable data perturbations. To find the maximally invariant data perturbation, we formulate the problem as linear programming. The experiment on the image classification with VGG16 shows that the proposed method could identify relevant parts of the images effectively.