Statistical Learning with Conditional Value at Risk
Paper and Code
Feb 14, 2020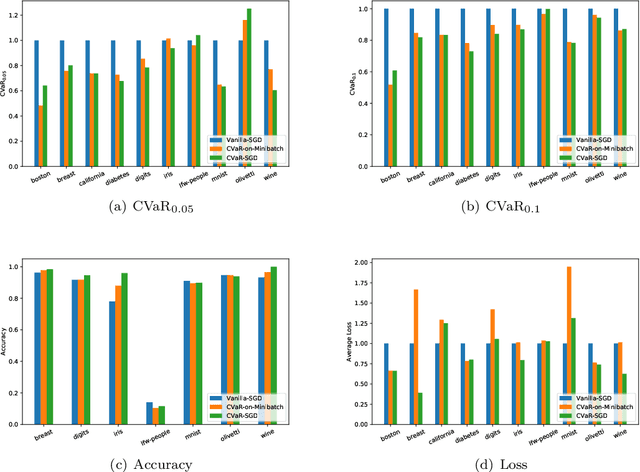
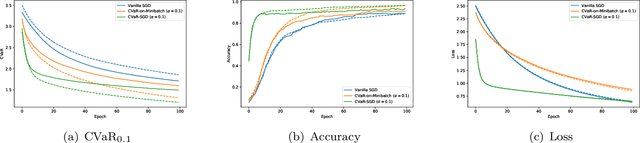
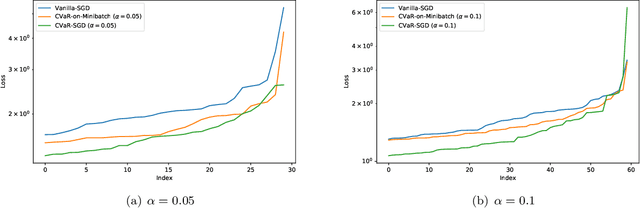
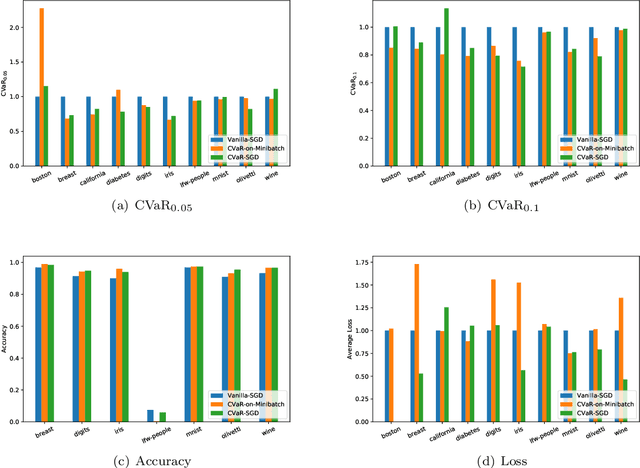
We propose a risk-averse statistical learning framework wherein the performance of a learning algorithm is evaluated by the conditional value-at-risk (CVaR) of losses rather than the expected loss. We devise algorithms based on stochastic gradient descent for this framework. While existing studies of CVaR optimization require direct access to the underlying distribution, our algorithms make a weaker assumption that only i.i.d.\ samples are given. For convex and Lipschitz loss functions, we show that our algorithm has $O(1/\sqrt{n})$-convergence to the optimal CVaR, where $n$ is the number of samples. For nonconvex and smooth loss functions, we show a generalization bound on CVaR. By conducting numerical experiments on various machine learning tasks, we demonstrate that our algorithms effectively minimize CVaR compared with other baseline algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge