A New Approach to Drifting Games, Based on Asymptotically Optimal Potentials

We develop a new approach to drifting games, a class of two-person games with many applications to boosting and online learning settings, including Prediction with Expert Advice and the Hedge game. Our approach involves (a) guessing an asymptotically optimal potential by solving an associated partial differential equation (PDE); then (b) justifying the guess, by proving upper and lower bounds on the final-time loss whose difference scales like a negative power of the number of time steps. The proofs of our potential-based upper bounds are elementary, using little more than Taylor expansion. The proofs of our potential-based lower bounds are also rather elementary, combining Taylor expansion with probabilistic or combinatorial arguments. Most previous work on asymptotically optimal strategies has used potentials obtained by solving a discrete dynamic programming principle; the arguments are complicated by their discrete nature. Our approach is facilitated by the fact that the potentials we use are explicit solutions of PDEs; the arguments are based on basic calculus. Not only is our approach more elementary, but we give new potentials and derive corresponding upper and lower bounds that match each other in the asymptotic regime.

Achieving Minimax Rates in Pool-Based Batch Active Learning

We consider a batch active learning scenario where the learner adaptively issues batches of points to a labeling oracle. Sampling labels in batches is highly desirable in practice due to the smaller number of interactive rounds with the labeling oracle (often human beings). However, batch active learning typically pays the price of a reduced adaptivity, leading to suboptimal results. In this paper we propose a solution which requires a careful trade off between the informativeness of the queried points and their diversity. We theoretically investigate batch active learning in the practically relevant scenario where the unlabeled pool of data is available beforehand (pool-based active learning). We analyze a novel stage-wise greedy algorithm and show that, as a function of the label complexity, the excess risk of this algorithm operating in the realizable setting for which we prove matches the known minimax rates in standard statistical learning settings. Our results also exhibit a mild dependence on the batch size. These are the first theoretical results that employ careful trade offs between informativeness and diversity to rigorously quantify the statistical performance of batch active learning in the pool-based scenario.

Neural Active Learning with Performance Guarantees

We investigate the problem of active learning in the streaming setting in non-parametric regimes, where the labels are stochastically generated from a class of functions on which we make no assumptions whatsoever. We rely on recently proposed Neural Tangent Kernel (NTK) approximation tools to construct a suitable neural embedding that determines the feature space the algorithm operates on and the learned model computed atop. Since the shape of the label requesting threshold is tightly related to the complexity of the function to be learned, which is a-priori unknown, we also derive a version of the algorithm which is agnostic to any prior knowledge. This algorithm relies on a regret balancing scheme to solve the resulting online model selection problem, and is computationally efficient. We prove joint guarantees on the cumulative regret and number of requested labels which depend on the complexity of the labeling function at hand. In the linear case, these guarantees recover known minimax results of the generalization error as a function of the label complexity in a standard statistical learning setting.

New Potential-Based Bounds for the Geometric-Stopping Version of Prediction with Expert Advice

This work addresses the classic machine learning problem of online prediction with expert advice. A potential-based framework for the fixed horizon version of this problem was previously developed using verification arguments from optimal control theory (Kobzar, Kohn and Wang, New Potential-Based Bounds for Prediction with Expert Advice (2019)). This paper extends this framework to the random (geometric) stopping version. Taking advantage of these ideas, we construct potentials for the geometric version of prediction with expert advice from potentials used for the fixed horizon version. This construction leads to new explicit lower and upper bounds associated with specific adversary and player strategies for the geometric problem. We identify regimes where these bounds are state of the art.

New Potential-Based Bounds for Prediction with Expert Advice

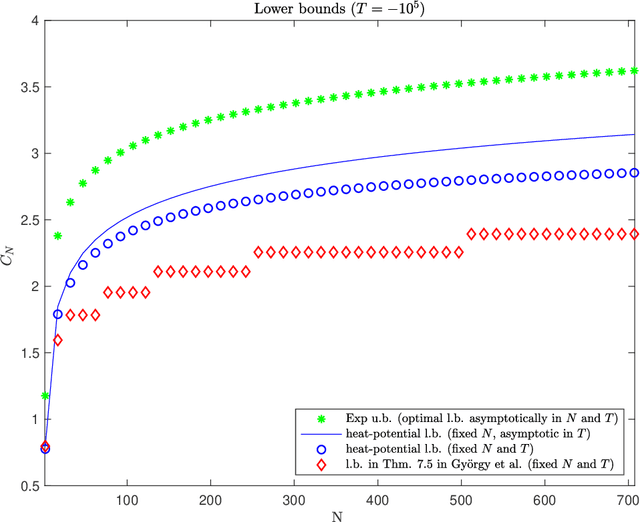
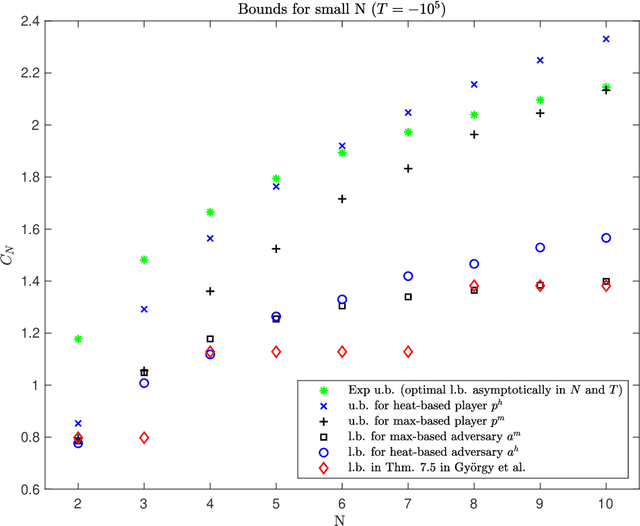
This work addresses the classic machine learning problem of online prediction with expert advice. We consider the finite-horizon version of this zero-sum, two-person game. Using verification arguments from optimal control theory, we view the task of finding better lower and upper bounds on the value of the game (regret) as the problem of finding better sub- and supersolutions of certain partial differential equations (PDEs). These sub- and supersolutions serve as the potentials for player and adversary strategies, which lead to the corresponding bounds. Our techniques extend in a nonasymptotic setting the recent work of Drenska and Kohn (J. Nonlinear Sci. 2019), which showed that the asymptotically optimal value function is the unique solution of an associated nonlinear PDE. To get explicit bounds, we use closed-form solutions of specific PDEs. Our bounds hold for any fixed number of experts and any time-horizon $T$; in certain regimes (which we identify) they improve upon the previous state-of-the-art. For up to three experts, our bounds provide the asymptotically optimal leading order term. Therefore, we provide a continuum perspective on recent work on optimal strategies for the case of $N \leq 3$ experts. We expect that our framework could be used to systematize and advance theory and applications of online learning in other settings as well.