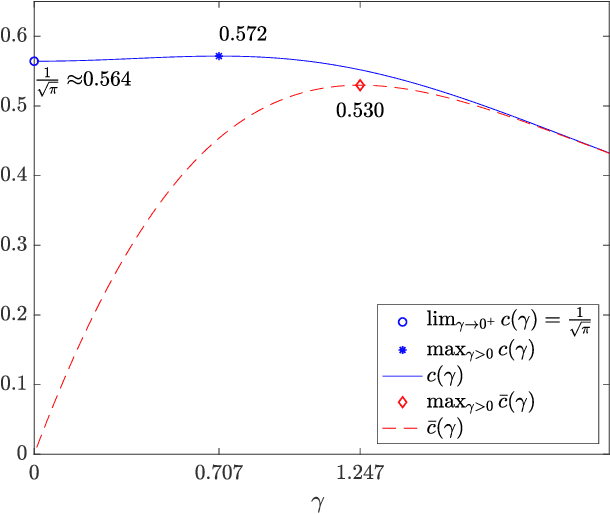
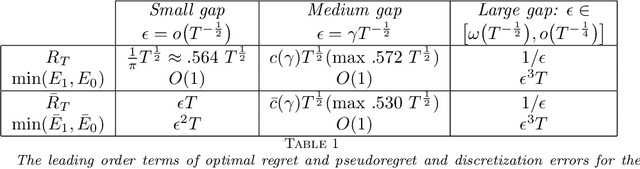
A PDE-Based Analysis of the Symmetric Two-Armed Bernoulli Bandit

This work addresses a version of the two-armed Bernoulli bandit problem where the sum of the means of the arms is one (the symmetric two-armed Bernoulli bandit). In a regime where the gap between these means goes to zero and the number of prediction periods approaches infinity, we obtain the leading order terms of the expected regret and pseudoregret for this problem by associating each of them with a solution of a linear parabolic partial differential equation. Our results improve upon the previously known results; specifically we explicitly compute the leading order term of the optimal regret and pseudoregret in three different scaling regimes for the gap. Additionally, we obtain new non-asymptotic bounds for any given time horizon.

New Potential-Based Bounds for the Geometric-Stopping Version of Prediction with Expert Advice

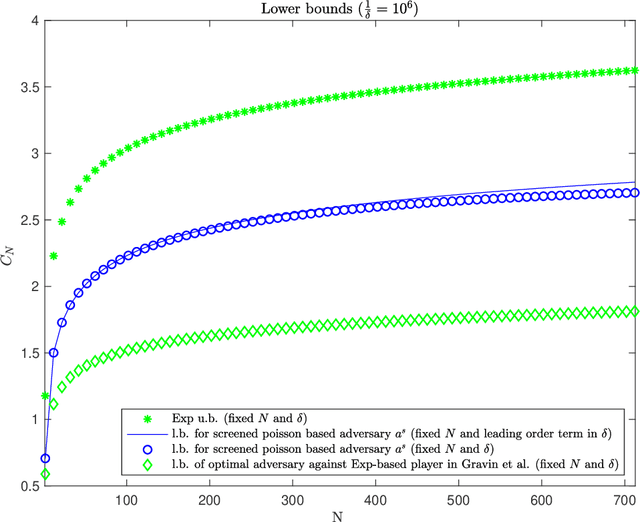
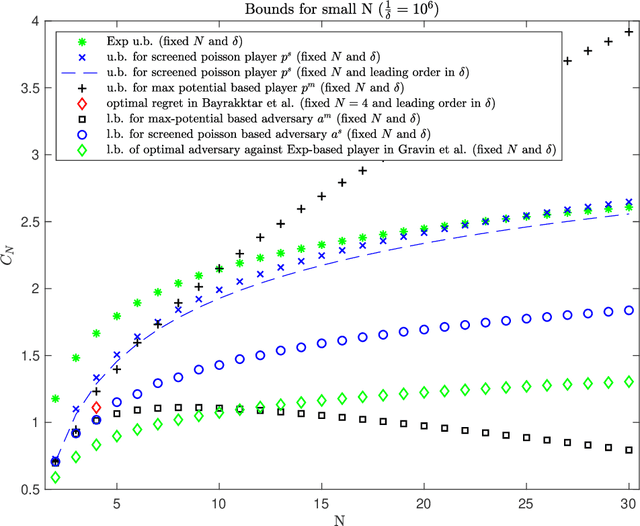
This work addresses the classic machine learning problem of online prediction with expert advice. A potential-based framework for the fixed horizon version of this problem was previously developed using verification arguments from optimal control theory (Kobzar, Kohn and Wang, New Potential-Based Bounds for Prediction with Expert Advice (2019)). This paper extends this framework to the random (geometric) stopping version. Taking advantage of these ideas, we construct potentials for the geometric version of prediction with expert advice from potentials used for the fixed horizon version. This construction leads to new explicit lower and upper bounds associated with specific adversary and player strategies for the geometric problem. We identify regimes where these bounds are state of the art.

New Potential-Based Bounds for Prediction with Expert Advice

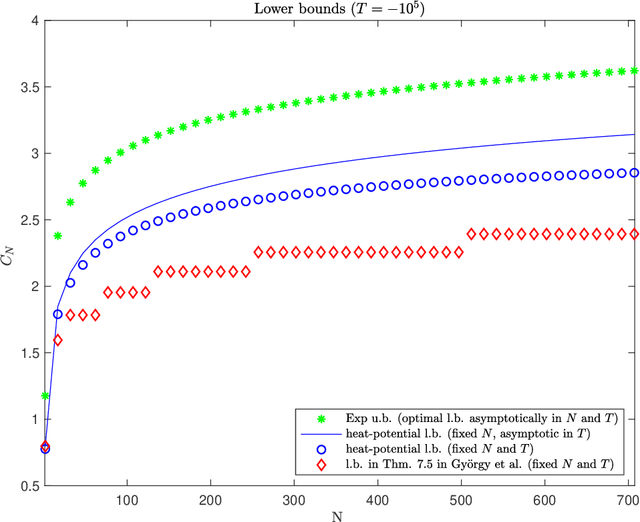
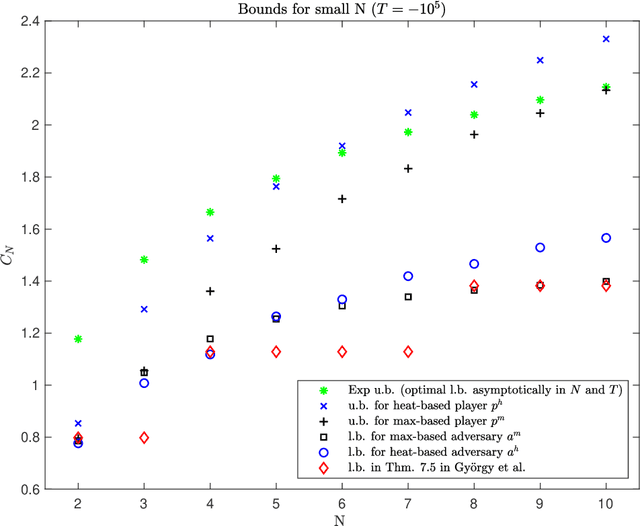
This work addresses the classic machine learning problem of online prediction with expert advice. We consider the finite-horizon version of this zero-sum, two-person game. Using verification arguments from optimal control theory, we view the task of finding better lower and upper bounds on the value of the game (regret) as the problem of finding better sub- and supersolutions of certain partial differential equations (PDEs). These sub- and supersolutions serve as the potentials for player and adversary strategies, which lead to the corresponding bounds. Our techniques extend in a nonasymptotic setting the recent work of Drenska and Kohn (J. Nonlinear Sci. 2019), which showed that the asymptotically optimal value function is the unique solution of an associated nonlinear PDE. To get explicit bounds, we use closed-form solutions of specific PDEs. Our bounds hold for any fixed number of experts and any time-horizon $T$; in certain regimes (which we identify) they improve upon the previous state-of-the-art. For up to three experts, our bounds provide the asymptotically optimal leading order term. Therefore, we provide a continuum perspective on recent work on optimal strategies for the case of $N \leq 3$ experts. We expect that our framework could be used to systematize and advance theory and applications of online learning in other settings as well.