New Potential-Based Bounds for the Geometric-Stopping Version of Prediction with Expert Advice

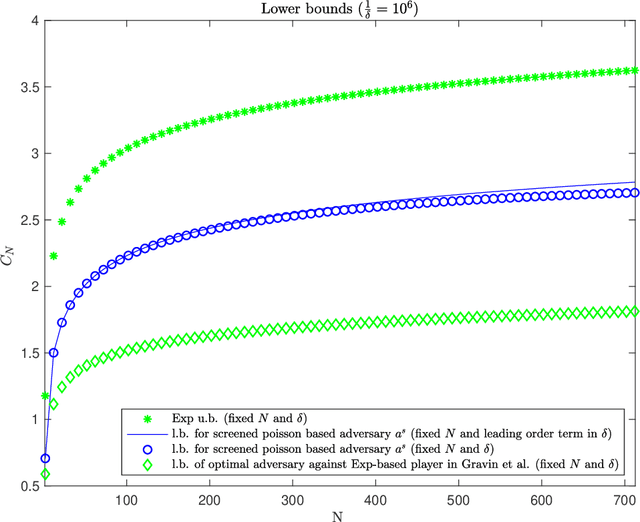
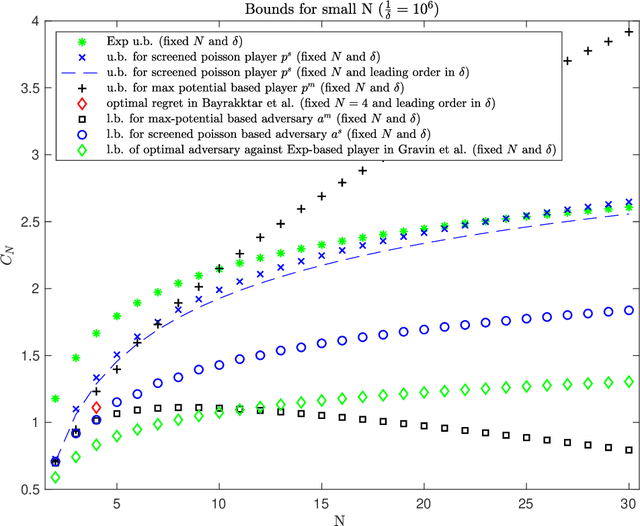
This work addresses the classic machine learning problem of online prediction with expert advice. A potential-based framework for the fixed horizon version of this problem was previously developed using verification arguments from optimal control theory (Kobzar, Kohn and Wang, New Potential-Based Bounds for Prediction with Expert Advice (2019)). This paper extends this framework to the random (geometric) stopping version. Taking advantage of these ideas, we construct potentials for the geometric version of prediction with expert advice from potentials used for the fixed horizon version. This construction leads to new explicit lower and upper bounds associated with specific adversary and player strategies for the geometric problem. We identify regimes where these bounds are state of the art.