New Potential-Based Bounds for Prediction with Expert Advice

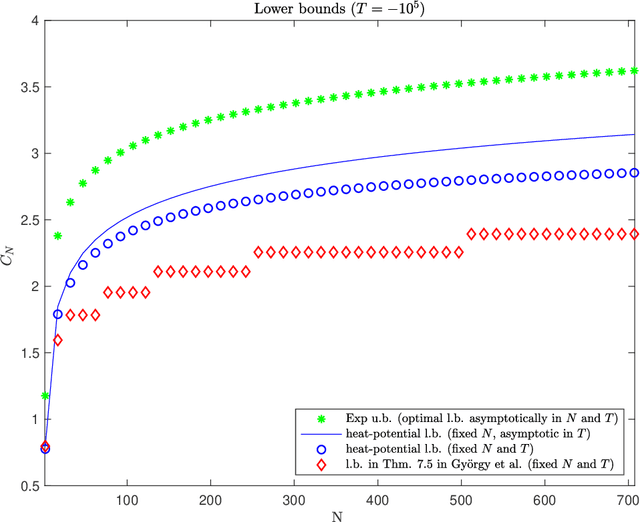
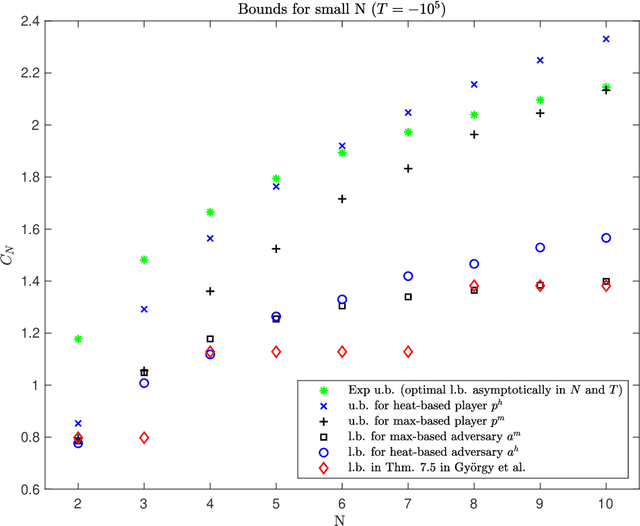
This work addresses the classic machine learning problem of online prediction with expert advice. We consider the finite-horizon version of this zero-sum, two-person game. Using verification arguments from optimal control theory, we view the task of finding better lower and upper bounds on the value of the game (regret) as the problem of finding better sub- and supersolutions of certain partial differential equations (PDEs). These sub- and supersolutions serve as the potentials for player and adversary strategies, which lead to the corresponding bounds. Our techniques extend in a nonasymptotic setting the recent work of Drenska and Kohn (J. Nonlinear Sci. 2019), which showed that the asymptotically optimal value function is the unique solution of an associated nonlinear PDE. To get explicit bounds, we use closed-form solutions of specific PDEs. Our bounds hold for any fixed number of experts and any time-horizon $T$; in certain regimes (which we identify) they improve upon the previous state-of-the-art. For up to three experts, our bounds provide the asymptotically optimal leading order term. Therefore, we provide a continuum perspective on recent work on optimal strategies for the case of $N \leq 3$ experts. We expect that our framework could be used to systematize and advance theory and applications of online learning in other settings as well.