Natural Policy Gradient for Average Reward Non-Stationary RL

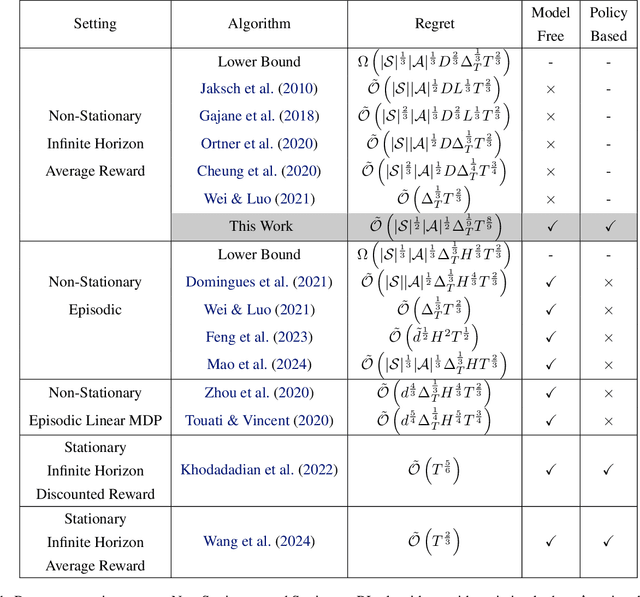
We consider the problem of non-stationary reinforcement learning (RL) in the infinite-horizon average-reward setting. We model it by a Markov Decision Process with time-varying rewards and transition probabilities, with a variation budget of $\Delta_T$. Existing non-stationary RL algorithms focus on model-based and model-free value-based methods. Policy-based methods despite their flexibility in practice are not theoretically well understood in non-stationary RL. We propose and analyze the first model-free policy-based algorithm, Non-Stationary Natural Actor-Critic (NS-NAC), a policy gradient method with a restart based exploration for change and a novel interpretation of learning rates as adapting factors. Further, we present a bandit-over-RL based parameter-free algorithm BORL-NS-NAC that does not require prior knowledge of the variation budget $\Delta_T$. We present a dynamic regret of $\tilde{\mathscr O}(|S|^{1/2}|A|^{1/2}\Delta_T^{1/6}T^{5/6})$ for both algorithms, where $T$ is the time horizon, and $|S|$, $|A|$ are the sizes of the state and action spaces. The regret analysis leverages a novel adaptation of the Lyapunov function analysis of NAC to dynamic environments and characterizes the effects of simultaneous updates in policy, value function estimate and changes in the environment.

Erasure Coded Neural Network Inference via Fisher Averaging

Erasure-coded computing has been successfully used in cloud systems to reduce tail latency caused by factors such as straggling servers and heterogeneous traffic variations. A majority of cloud computing traffic now consists of inference on neural networks on shared resources where the response time of inference queries is also adversely affected by the same factors. However, current erasure coding techniques are largely focused on linear computations such as matrix-vector and matrix-matrix multiplications and hence do not work for the highly non-linear neural network functions. In this paper, we seek to design a method to code over neural networks, that is, given two or more neural network models, how to construct a coded model whose output is a linear combination of the outputs of the given neural networks. We formulate the problem as a KL barycenter problem and propose a practical algorithm COIN that leverages the diagonal Fisher information to create a coded model that approximately outputs the desired linear combination of outputs. We conduct experiments to perform erasure coding over neural networks trained on real-world vision datasets and show that the accuracy of the decoded outputs using COIN is significantly higher than other baselines while being extremely compute-efficient.

Efficient Reinforcement Learning for Routing Jobs in Heterogeneous Queueing Systems

We consider the problem of efficiently routing jobs that arrive into a central queue to a system of heterogeneous servers. Unlike homogeneous systems, a threshold policy, that routes jobs to the slow server(s) when the queue length exceeds a certain threshold, is known to be optimal for the one-fast-one-slow two-server system. But an optimal policy for the multi-server system is unknown and non-trivial to find. While Reinforcement Learning (RL) has been recognized to have great potential for learning policies in such cases, our problem has an exponentially large state space size, rendering standard RL inefficient. In this work, we propose ACHQ, an efficient policy gradient based algorithm with a low dimensional soft threshold policy parameterization that leverages the underlying queueing structure. We provide stationary-point convergence guarantees for the general case and despite the low-dimensional parameterization prove that ACHQ converges to an approximate global optimum for the special case of two servers. Simulations demonstrate an improvement in expected response time of up to ~30% over the greedy policy that routes to the fastest available server.

Greedy $k$-Center from Noisy Distance Samples

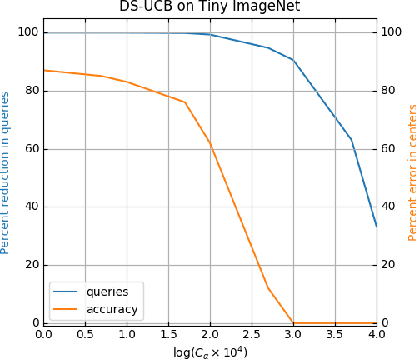
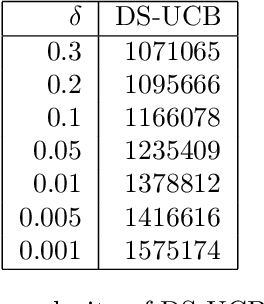
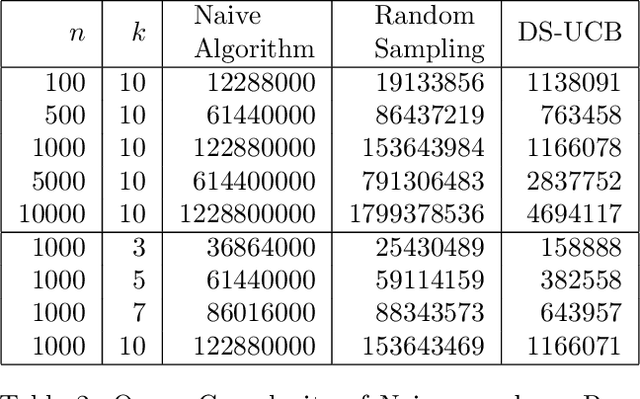
We study a variant of the canonical $k$-center problem over a set of vertices in a metric space, where the underlying distances are apriori unknown. Instead, we can query an oracle which provides noisy/incomplete estimates of the distance between any pair of vertices. We consider two oracle models: Dimension Sampling where each query to the oracle returns the distance between a pair of points in one dimension; and Noisy Distance Sampling where the oracle returns the true distance corrupted by noise. We propose active algorithms, based on ideas such as UCB and Thompson sampling developed in the closely related Multi-Armed Bandit problem, which adaptively decide which queries to send to the oracle and are able to solve the $k$-center problem within an approximation ratio of two with high probability. We analytically characterize instance-dependent query complexity of our algorithms and also demonstrate significant improvements over naive implementations via numerical evaluations on two real-world datasets (Tiny ImageNet and UT Zappos50K).