Toy-GS: Assembling Local Gaussians for Precisely Rendering Large-Scale Free Camera Trajectories

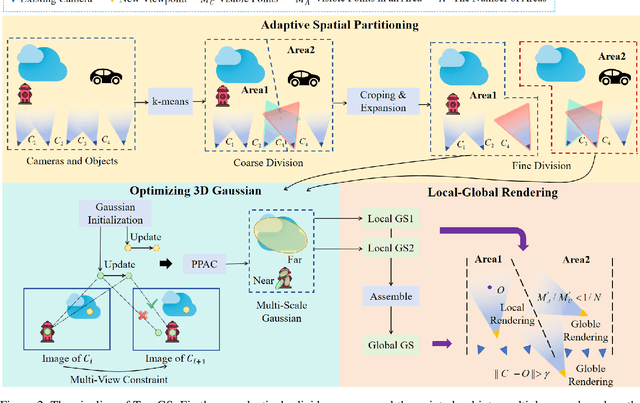
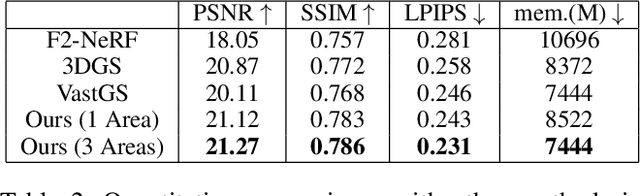
Currently, 3D rendering for large-scale free camera trajectories, namely, arbitrary input camera trajectories, poses significant challenges: 1) The distribution and observation angles of the cameras are irregular, and various types of scenes are included in the free trajectories; 2) Processing the entire point cloud and all images at once for large-scale scenes requires a substantial amount of GPU memory. This paper presents a Toy-GS method for accurately rendering large-scale free camera trajectories. Specifically, we propose an adaptive spatial division approach for free trajectories to divide cameras and the sparse point cloud of the entire scene into various regions according to camera poses. Training each local Gaussian in parallel for each area enables us to concentrate on texture details and minimize GPU memory usage. Next, we use the multi-view constraint and position-aware point adaptive control (PPAC) to improve the rendering quality of texture details. In addition, our regional fusion approach combines local and global Gaussians to enhance rendering quality with an increasing number of divided areas. Extensive experiments have been carried out to confirm the effectiveness and efficiency of Toy-GS, leading to state-of-the-art results on two public large-scale datasets as well as our SCUTic dataset. Our proposal demonstrates an enhancement of 1.19 dB in PSNR and conserves 7 G of GPU memory when compared to various benchmarks.

Debiasing Federated Learning with Correlated Client Participation

In cross-device federated learning (FL) with millions of mobile clients, only a small subset of clients participate in training in every communication round, and Federated Averaging (FedAvg) is the most popular algorithm in practice. Existing analyses of FedAvg usually assume the participating clients are independently sampled in each round from a uniform distribution, which does not reflect real-world scenarios. This paper introduces a theoretical framework that models client participation in FL as a Markov chain to study optimization convergence when clients have non-uniform and correlated participation across rounds. We apply this framework to analyze a more general and practical pattern: every client must wait a minimum number of $R$ rounds (minimum separation) before re-participating. We theoretically prove and empirically observe that increasing minimum separation reduces the bias induced by intrinsic non-uniformity of client availability in cross-device FL systems. Furthermore, we develop an effective debiasing algorithm for FedAvg that provably converges to the unbiased optimal solution under arbitrary minimum separation and unknown client availability distribution.

Aerial-NeRF: Adaptive Spatial Partitioning and Sampling for Large-Scale Aerial Rendering

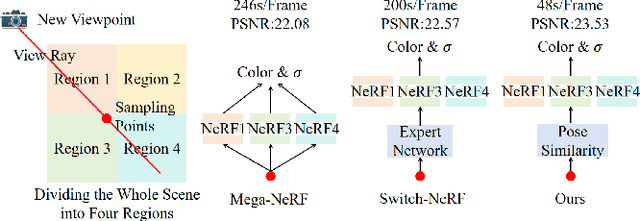
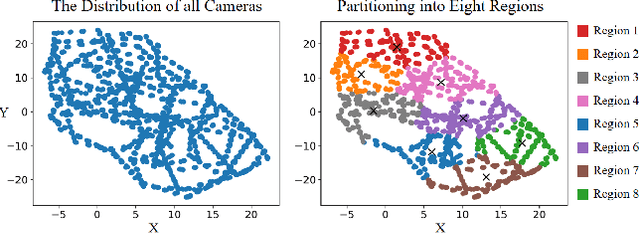
Recent progress in large-scale scene rendering has yielded Neural Radiance Fields (NeRF)-based models with an impressive ability to synthesize scenes across small objects and indoor scenes. Nevertheless, extending this idea to large-scale aerial rendering poses two critical problems. Firstly, a single NeRF cannot render the entire scene with high-precision for complex large-scale aerial datasets since the sampling range along each view ray is insufficient to cover buildings adequately. Secondly, traditional NeRFs are infeasible to train on one GPU to enable interactive fly-throughs for modeling massive images. Instead, existing methods typically separate the whole scene into multiple regions and train a NeRF on each region, which are unaccustomed to different flight trajectories and difficult to achieve fast rendering. To that end, we propose Aerial-NeRF with three innovative modifications for jointly adapting NeRF in large-scale aerial rendering: (1) Designing an adaptive spatial partitioning and selection method based on drones' poses to adapt different flight trajectories; (2) Using similarity of poses instead of (expert) network for rendering speedup to determine which region a new viewpoint belongs to; (3) Developing an adaptive sampling approach for rendering performance improvement to cover the entire buildings at different heights. Extensive experiments have conducted to verify the effectiveness and efficiency of Aerial-NeRF, and new state-of-the-art results have been achieved on two public large-scale aerial datasets and presented SCUTic dataset. Note that our model allows us to perform rendering over 4 times as fast as compared to multiple competitors. Our dataset, code, and model are publicly available at https://drliuqi.github.io/.

A Stochastic Quasi-Newton Method for Non-convex Optimization with Non-uniform Smoothness

Classical convergence analyses for optimization algorithms rely on the widely-adopted uniform smoothness assumption. However, recent experimental studies have demonstrated that many machine learning problems exhibit non-uniform smoothness, meaning the smoothness factor is a function of the model parameter instead of a universal constant. In particular, it has been observed that the smoothness grows with respect to the gradient norm along the training trajectory. Motivated by this phenomenon, the recently introduced $(L_0, L_1)$-smoothness is a more general notion, compared to traditional $L$-smoothness, that captures such positive relationship between smoothness and gradient norm. Under this type of non-uniform smoothness, existing literature has designed stochastic first-order algorithms by utilizing gradient clipping techniques to obtain the optimal $\mathcal{O}(\epsilon^{-3})$ sample complexity for finding an $\epsilon$-approximate first-order stationary solution. Nevertheless, the studies of quasi-Newton methods are still lacking. Considering higher accuracy and more robustness for quasi-Newton methods, in this paper we propose a fast stochastic quasi-Newton method when there exists non-uniformity in smoothness. Leveraging gradient clipping and variance reduction, our algorithm can achieve the best-known $\mathcal{O}(\epsilon^{-3})$ sample complexity and enjoys convergence speedup with simple hyperparameter tuning. Our numerical experiments show that our proposed algorithm outperforms the state-of-the-art approaches.

Machine-Learning-Assisted and Real-Time-Feedback-Controlled Growth of InAs/GaAs Quantum Dots

Self-assembled InAs/GaAs quantum dots (QDs) have properties highly valuable for developing various optoelectronic devices such as QD lasers and single photon sources. The applications strongly rely on the density and quality of these dots, which has motivated studies of the growth process control to realize high-quality epi-wafers and devices. Establishing the process parameters in molecular beam epitaxy (MBE) for a specific density of QDs is a multidimensional optimization challenge, usually addressed through time-consuming and iterative trial-and-error. Here, we report a real-time feedback control method to realize the growth of QDs with arbitrary and precise density, which is fully automated and intelligent. We developed a machine learning (ML) model named 3D ResNet, specially designed for training RHEED videos instead of static images and providing real-time feedback on surface morphologies for process control. As a result, we demonstrated that ML from previous growth could predict the post-growth density of QDs, by successfully tuning the QD densities in near-real time from 1.5E10 cm-2 down to 3.8E8 cm-2 or up to 1.4E11 cm-2. Compared to traditional methods, our approach, with in-situ tuning capabilities and excellent reliability, can dramatically expedite the material optimization process and improve the reproducibility of MBE growth, constituting significant progress for thin film growth techniques. The concepts and methodologies proved feasible in this work are promising to be applied to a variety of material growth processes, which will revolutionize semiconductor manufacturing for microelectronic and optoelectronic industries.

SUGAR: Spherical Ultrafast Graph Attention Framework for Cortical Surface Registration

Cortical surface registration plays a crucial role in aligning cortical functional and anatomical features across individuals. However, conventional registration algorithms are computationally inefficient. Recently, learning-based registration algorithms have emerged as a promising solution, significantly improving processing efficiency. Nonetheless, there remains a gap in the development of a learning-based method that exceeds the state-of-the-art conventional methods simultaneously in computational efficiency, registration accuracy, and distortion control, despite the theoretically greater representational capabilities of deep learning approaches. To address the challenge, we present SUGAR, a unified unsupervised deep-learning framework for both rigid and non-rigid registration. SUGAR incorporates a U-Net-based spherical graph attention network and leverages the Euler angle representation for deformation. In addition to the similarity loss, we introduce fold and multiple distortion losses, to preserve topology and minimize various types of distortions. Furthermore, we propose a data augmentation strategy specifically tailored for spherical surface registration, enhancing the registration performance. Through extensive evaluation involving over 10,000 scans from 7 diverse datasets, we showed that our framework exhibits comparable or superior registration performance in accuracy, distortion, and test-retest reliability compared to conventional and learning-based methods. Additionally, SUGAR achieves remarkable sub-second processing times, offering a notable speed-up of approximately 12,000 times in registering 9,000 subjects from the UK Biobank dataset in just 32 minutes. This combination of high registration performance and accelerated processing time may greatly benefit large-scale neuroimaging studies.

Understanding Generalization of Federated Learning via Stability: Heterogeneity Matters

Generalization performance is a key metric in evaluating machine learning models when applied to real-world applications. Good generalization indicates the model can predict unseen data correctly when trained under a limited number of data. Federated learning (FL), which has emerged as a popular distributed learning framework, allows multiple devices or clients to train a shared model without violating privacy requirements. While the existing literature has studied extensively the generalization performances of centralized machine learning algorithms, similar analysis in the federated settings is either absent or with very restrictive assumptions on the loss functions. In this paper, we aim to analyze the generalization performances of federated learning by means of algorithmic stability, which measures the change of the output model of an algorithm when perturbing one data point. Three widely-used algorithms are studied, including FedAvg, SCAFFOLD, and FedProx, under convex and non-convex loss functions. Our analysis shows that the generalization performances of models trained by these three algorithms are closely related to the heterogeneity of clients' datasets as well as the convergence behaviors of the algorithms. Particularly, in the i.i.d. setting, our results recover the classical results of stochastic gradient descent (SGD).

A Communication-efficient Algorithm with Linear Convergence for Federated Minimax Learning

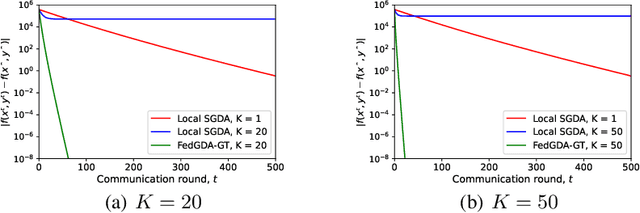
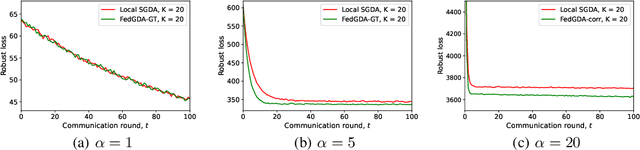
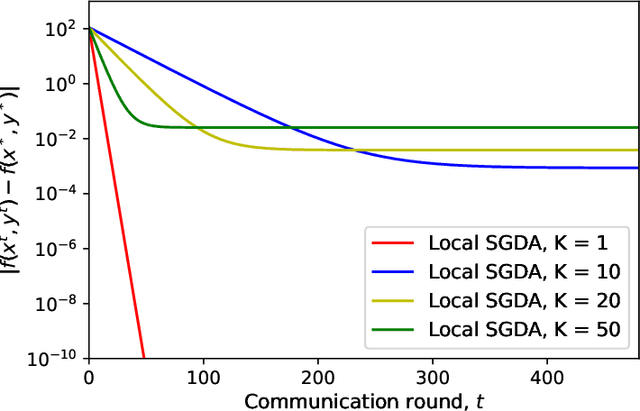
In this paper, we study a large-scale multi-agent minimax optimization problem, which models many interesting applications in statistical learning and game theory, including Generative Adversarial Networks (GANs). The overall objective is a sum of agents' private local objective functions. We first analyze an important special case, empirical minimax problem, where the overall objective approximates a true population minimax risk by statistical samples. We provide generalization bounds for learning with this objective through Rademacher complexity analysis. Then, we focus on the federated setting, where agents can perform local computation and communicate with a central server. Most existing federated minimax algorithms either require communication per iteration or lack performance guarantees with the exception of Local Stochastic Gradient Descent Ascent (SGDA), a multiple-local-update descent ascent algorithm which guarantees convergence under a diminishing stepsize. By analyzing Local SGDA under the ideal condition of no gradient noise, we show that generally it cannot guarantee exact convergence with constant stepsizes and thus suffers from slow rates of convergence. To tackle this issue, we propose FedGDA-GT, an improved Federated (Fed) Gradient Descent Ascent (GDA) method based on Gradient Tracking (GT). When local objectives are Lipschitz smooth and strongly-convex-strongly-concave, we prove that FedGDA-GT converges linearly with a constant stepsize to global $\epsilon$-approximation solution with $\mathcal{O}(\log (1/\epsilon))$ rounds of communication, which matches the time complexity of centralized GDA method. Finally, we numerically show that FedGDA-GT outperforms Local SGDA.