Fine-grained Analysis of In-context Linear Estimation: Data, Architecture, and Beyond
Paper and Code
Jul 13, 2024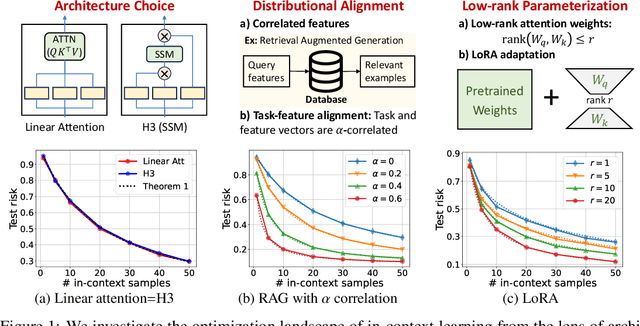
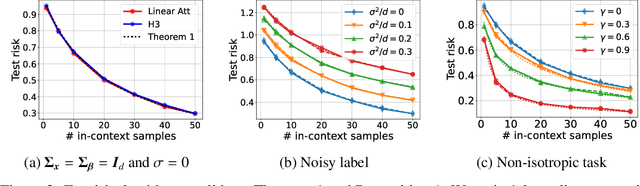
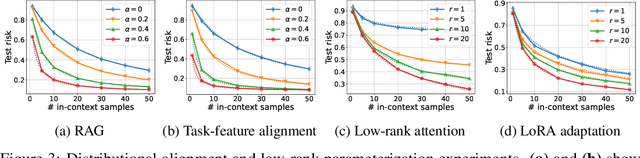
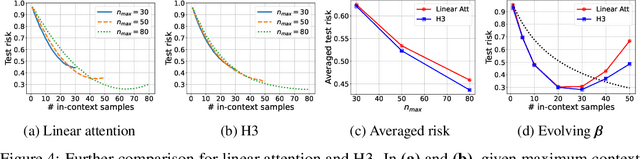
Recent research has shown that Transformers with linear attention are capable of in-context learning (ICL) by implementing a linear estimator through gradient descent steps. However, the existing results on the optimization landscape apply under stylized settings where task and feature vectors are assumed to be IID and the attention weights are fully parameterized. In this work, we develop a stronger characterization of the optimization and generalization landscape of ICL through contributions on architectures, low-rank parameterization, and correlated designs: (1) We study the landscape of 1-layer linear attention and 1-layer H3, a state-space model. Under a suitable correlated design assumption, we prove that both implement 1-step preconditioned gradient descent. We show that thanks to its native convolution filters, H3 also has the advantage of implementing sample weighting and outperforming linear attention in suitable settings. (2) By studying correlated designs, we provide new risk bounds for retrieval augmented generation (RAG) and task-feature alignment which reveal how ICL sample complexity benefits from distributional alignment. (3) We derive the optimal risk for low-rank parameterized attention weights in terms of covariance spectrum. Through this, we also shed light on how LoRA can adapt to a new distribution by capturing the shift between task covariances. Experimental results corroborate our theoretical findings. Overall, this work explores the optimization and risk landscape of ICL in practically meaningful settings and contributes to a more thorough understanding of its mechanics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge