Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Chuhan Xie
Asymptotic Time-Uniform Inference for Parameters in Averaged Stochastic Approximation
Oct 19, 2024Figures and Tables: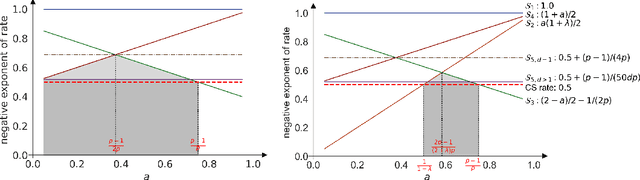

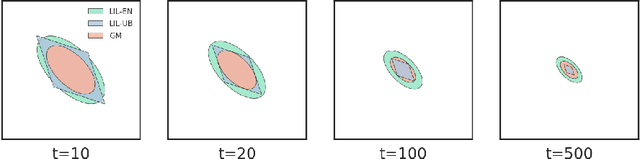
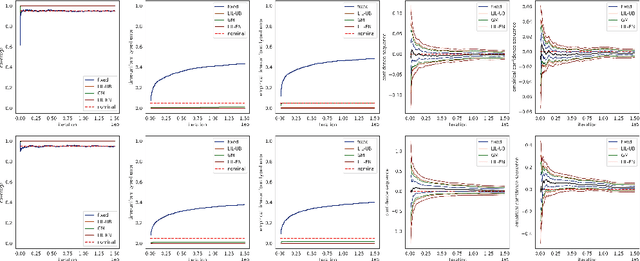




Abstract:We study time-uniform statistical inference for parameters in stochastic approximation (SA), which encompasses a bunch of applications in optimization and machine learning. To that end, we analyze the almost-sure convergence rates of the averaged iterates to a scaled sum of Gaussians in both linear and nonlinear SA problems. We then construct three types of asymptotic confidence sequences that are valid uniformly across all times with coverage guarantees, in an asymptotic sense that the starting time is sufficiently large. These coverage guarantees remain valid if the unknown covariance matrix is replaced by its plug-in estimator, and we conduct experiments to validate our methodology.
* 35 pages, 4 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge