Online Statistical Inference for Nonlinear Stochastic Approximation with Markovian Data
Paper and Code
Feb 20, 2023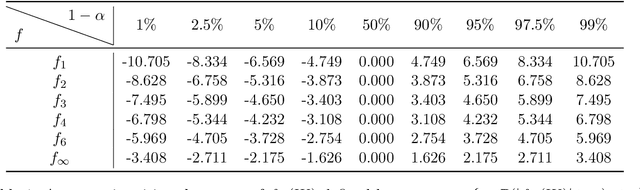
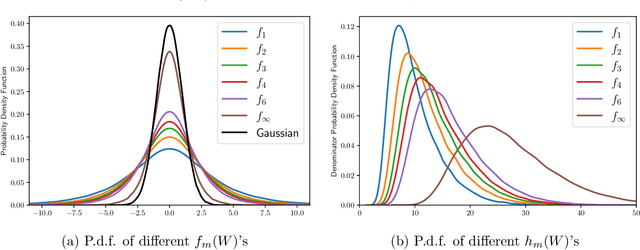
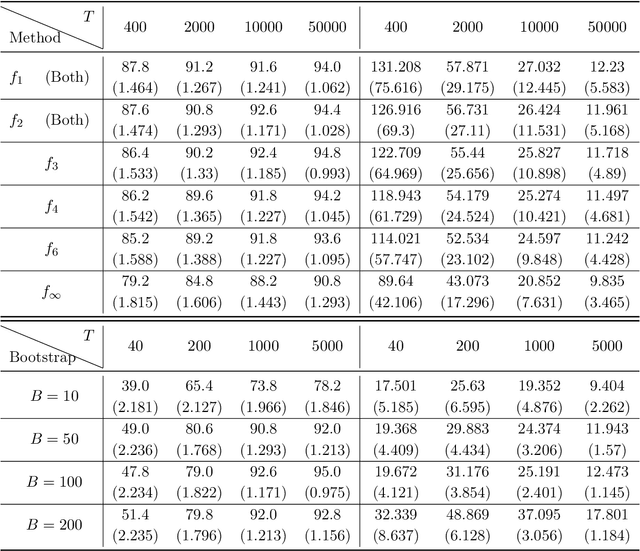
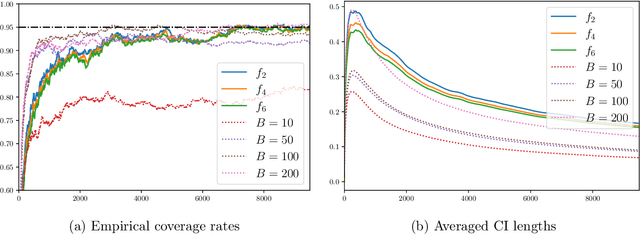
We study the statistical inference of nonlinear stochastic approximation algorithms utilizing a single trajectory of Markovian data. Our methodology has practical applications in various scenarios, such as Stochastic Gradient Descent (SGD) on autoregressive data and asynchronous Q-Learning. By utilizing the standard stochastic approximation (SA) framework to estimate the target parameter, we establish a functional central limit theorem for its partial-sum process, $\boldsymbol{\phi}_T$. To further support this theory, we provide a matching semiparametric efficient lower bound and a non-asymptotic upper bound on its weak convergence, measured in the L\'evy-Prokhorov metric. This functional central limit theorem forms the basis for our inference method. By selecting any continuous scale-invariant functional $f$, the asymptotic pivotal statistic $f(\boldsymbol{\phi}_T)$ becomes accessible, allowing us to construct an asymptotically valid confidence interval. We analyze the rejection probability of a family of functionals $f_m$, indexed by $m \in \mathbb{N}$, through theoretical and numerical means. The simulation results demonstrate the validity and efficiency of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge