Finding the Near Optimal Policy via Adaptive Reduced Regularization in MDPs
Paper and Code
Oct 31, 2020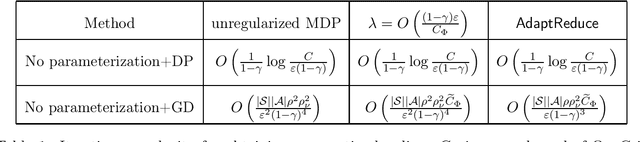
Regularized MDPs serve as a smooth version of original MDPs. However, biased optimal policy always exists for regularized MDPs. Instead of making the coefficient{\lambda}of regularized term sufficiently small, we propose an adaptive reduction scheme for {\lambda} to approximate optimal policy of the original MDP. It is shown that the iteration complexity for obtaining an{\epsilon}-optimal policy could be reduced in comparison with setting sufficiently small{\lambda}. In addition, there exists strong duality connection between the reduction method and solving the original MDP directly, from which we can derive more adaptive reduction method for certain algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge