DIPPA: An improved Method for Bilinear Saddle Point Problems
Paper and Code
Mar 15, 2021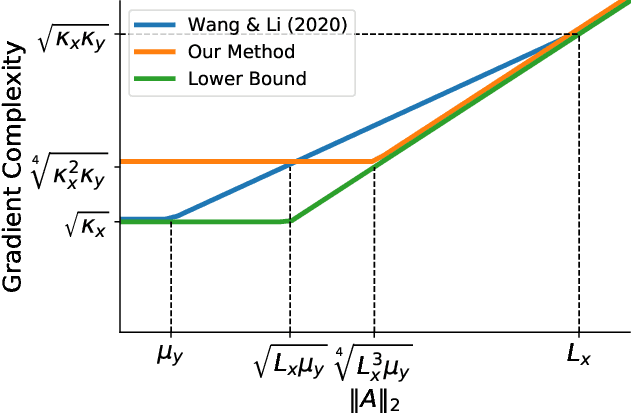

This paper studies bilinear saddle point problems $\min_{\bf{x}} \max_{\bf{y}} g(\bf{x}) + \bf{x}^{\top} \bf{A} \bf{y} - h(\bf{y})$, where the functions $g, h$ are smooth and strongly-convex. When the gradient and proximal oracle related to $g$ and $h$ are accessible, optimal algorithms have already been developed in the literature \cite{chambolle2011first, palaniappan2016stochastic}. However, the proximal operator is not always easy to compute, especially in constraint zero-sum matrix games \cite{zhang2020sparsified}. This work proposes a new algorithm which only requires the access to the gradients of $g, h$. Our algorithm achieves a complexity upper bound $\tilde{\mathcal{O}}\left( \frac{\|\bf{A}\|_2}{\sqrt{\mu_x \mu_y}} + \sqrt[4]{\kappa_x \kappa_y (\kappa_x + \kappa_y)} \right)$ which has optimal dependency on the coupling condition number $\frac{\|\bf{A}\|_2}{\sqrt{\mu_x \mu_y}}$ up to logarithmic factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge