Zohar Nussinov
Transform then Explore: a Simple and Effective Technique for Exploratory Combinatorial Optimization with Reinforcement Learning
Apr 06, 2024Abstract:Many complex problems encountered in both production and daily life can be conceptualized as combinatorial optimization problems (COPs) over graphs. Recent years, reinforcement learning (RL) based models have emerged as a promising direction, which treat the COPs solving as a heuristic learning problem. However, current finite-horizon-MDP based RL models have inherent limitations. They are not allowed to explore adquately for improving solutions at test time, which may be necessary given the complexity of NP-hard optimization tasks. Some recent attempts solve this issue by focusing on reward design and state feature engineering, which are tedious and ad-hoc. In this work, we instead propose a much simpler but more effective technique, named gauge transformation (GT). The technique is originated from physics, but is very effective in enabling RL agents to explore to continuously improve the solutions during test. Morever, GT is very simple, which can be implemented with less than 10 lines of Python codes, and can be applied to a vast majority of RL models. Experimentally, we show that traditional RL models with GT technique produce the state-of-the-art performances on the MaxCut problem. Furthermore, since GT is independent of any RL models, it can be seamlessly integrated into various RL frameworks, paving the way of these models for more effective explorations in the solving of general COPs.
A new nature inspired modularity function adapted for unsupervised learning involving spatially embedded networks: A comparative analysis
Jul 18, 2020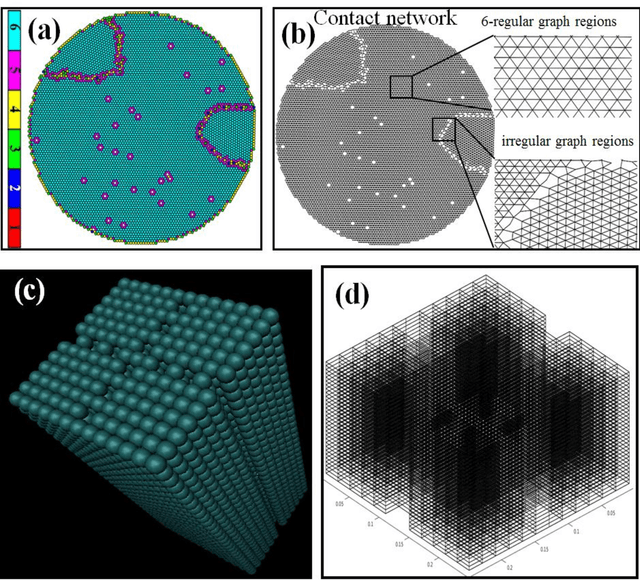

Abstract:Unsupervised machine learning methods can be of great help in many traditional engineering disciplines, where huge amount of labeled data is not readily available or is extremely difficult or costly to generate. Two specific examples include the structure of granular materials and atomic structure of metallic glasses. While the former is critically important for several hundreds of billion dollars global industries, the latter is still a big puzzle in fundamental science. One thing is common in both the examples is that the particles are the elements of the ensembles that are embedded in Euclidean space and one can create a spatially embedded network to represent their key features. Some recent studies show that clustering, which generically refers to unsupervised learning, holds great promise in partitioning these networks. In many complex networks, the spatial information of nodes play very important role in determining the network properties. So understanding the structure of such networks is very crucial. We have compared the performance of our newly developed modularity function with some of the well-known modularity functions. We performed this comparison by finding the best partition in 2D and 3D granular assemblies. We show that for the class of networks considered in this article, our method produce much better results than the competing methods.
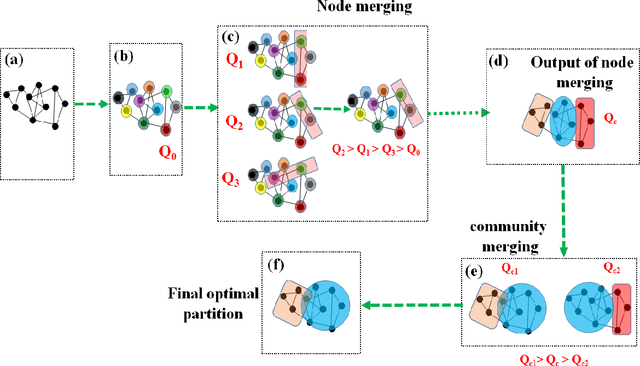
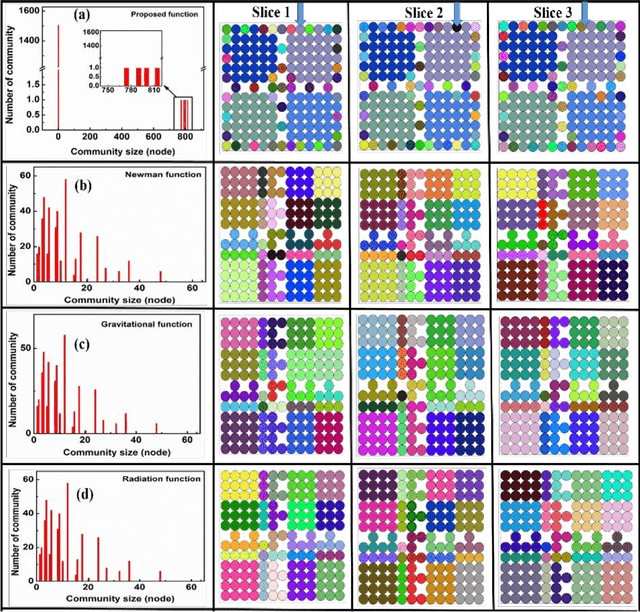
Unsupervised Community Detection with a Potts Model Hamiltonian, an Efficient Algorithmic Solution, and Applications in Digital Pathology
Feb 05, 2020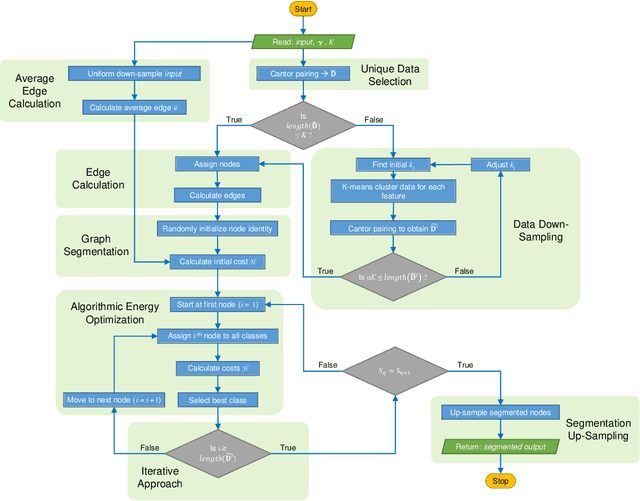
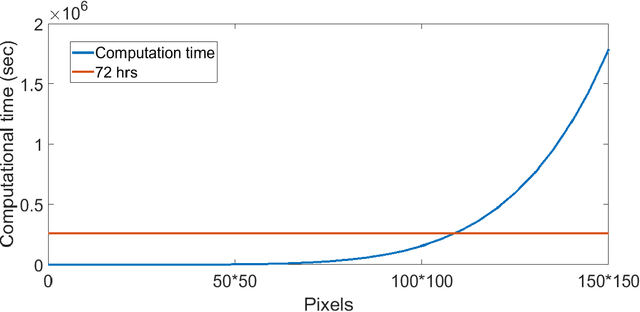
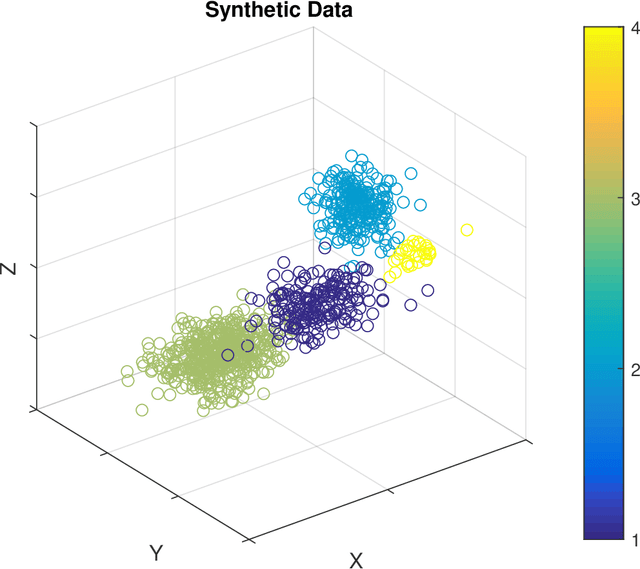
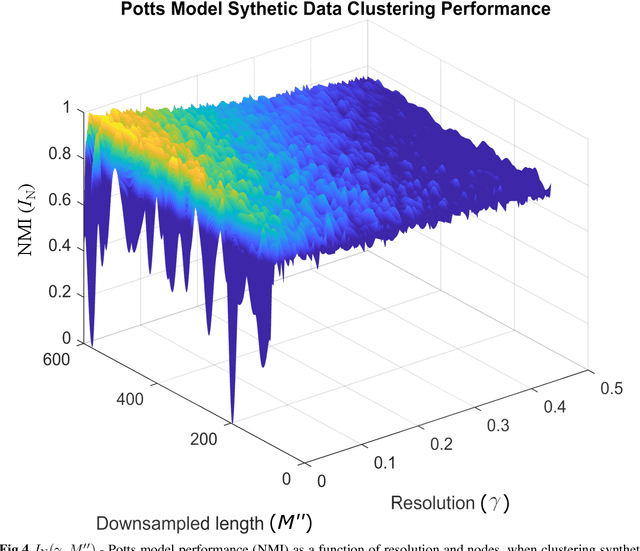
Abstract:Unsupervised segmentation of large images using a Potts model Hamiltonian is unique in that segmentation is governed by a resolution parameter which scales the sensitivity to small clusters. Here, the input image is first modeled as a graph, which is then segmented by minimizing a Hamiltonian cost function defined on the graph and the respective segments. However, there exists no closed form solution of this optimization, and using previous iterative algorithmic solution techniques, the problem scales quadratically in the Input Length. Therefore, while Potts model segmentation gives accurate segmentation, it is grossly underutilized as an unsupervised learning technique. We propose a fast statistical down-sampling of input image pixels based on the respective color features, and a new iterative method to minimize the Potts model energy considering pixel to segment relationship. This method is generalizable and can be extended for image pixel texture features as well as spatial features. We demonstrate that this new method is highly efficient, and outperforms existing methods for Potts model based image segmentation. We demonstrate the application of our method in medical microscopy image segmentation; particularly, in segmenting renal glomerular micro-environment in renal pathology. Our method is not limited to image segmentation, and can be extended to any image/data segmentation/clustering task for arbitrary datasets with discrete features.
Visual Machine Learning: Insight through Eigenvectors, Chladni patterns and community detection in 2D particulate structures
Jan 02, 2020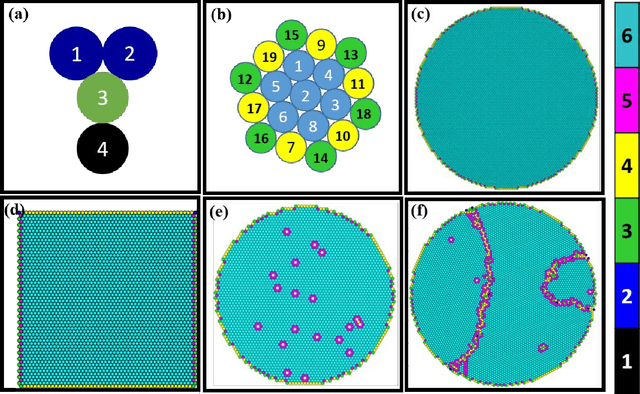

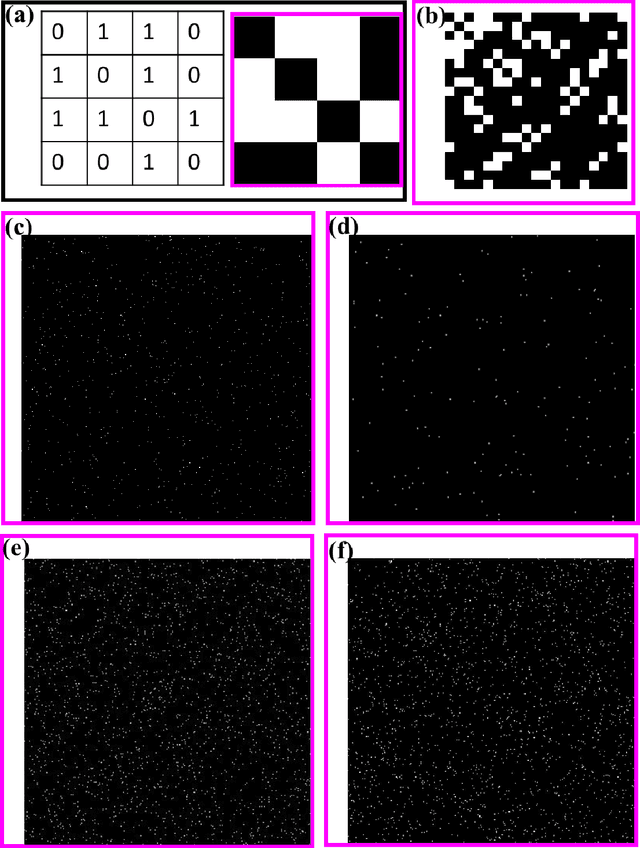
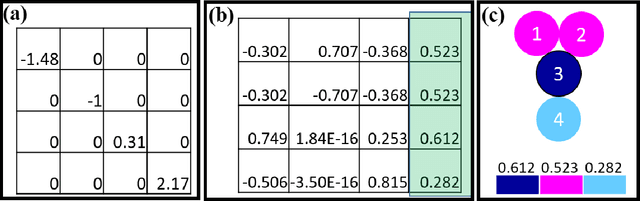
Abstract:Machine learning (ML) is quickly emerging as a powerful tool with diverse applications across an extremely broad spectrum of disciplines and commercial endeavors. Typically, ML is used as a black box that provides little illuminating rationalization of its output. In the current work, we aim to better understand the generic intuition underlying unsupervised ML with a focus on physical systems. The systems that are studied here as test cases comprise of six different 2-dimensional (2-D) particulate systems of different complexities. It is noted that the findings of this study are generic to any unsupervised ML problem and are not restricted to materials systems alone. Three rudimentary unsupervised ML techniques are employed on the adjacency (connectivity) matrix of the six studied systems: (i) using principal eigenvalue and eigenvectors of the adjacency matrix, (ii) spectral decomposition, and (iii) a Potts model based community detection technique in which a modularity function is maximized. We demonstrate that, while solving a completely classical problem, ML technique produces features that are distinctly connected to quantum mechanical solutions. Dissecting these features help us to understand the deep connection between the classical non-linear world and the quantum mechanical linear world through the kaleidoscope of ML technique, which might have far reaching consequences both in the arena of physical sciences and ML.
The Stochastic Replica Approach to Machine Learning: Stability and Parameter Optimization
Oct 13, 2017



Abstract:We introduce a statistical physics inspired supervised machine learning algorithm for classification and regression problems. The method is based on the invariances or stability of predicted results when known data is represented as expansions in terms of various stochastic functions. The algorithm predicts the classification/regression values of new data by combining (via voting) the outputs of these numerous linear expansions in randomly chosen functions. The few parameters (typically only one parameter is used in all studied examples) that this model has may be automatically optimized. The algorithm has been tested on 10 diverse training data sets of various types and feature space dimensions. It has been shown to consistently exhibit high accuracy and readily allow for optimization of parameters, while simultaneously avoiding pitfalls of existing algorithms such as those associated with class imbalance. We very briefly speculate on whether spatial coordinates in physical theories may be viewed as emergent "features" that enable a robust machine learning type description of data with generic low order smooth functions.
An interacting replica approach applied to the traveling salesman problem
Mar 14, 2016



Abstract:We present a physics inspired heuristic method for solving combinatorial optimization problems. Our approach is specifically motivated by the desire to avoid trapping in metastable local minima- a common occurrence in hard problems with multiple extrema. Our method involves (i) coupling otherwise independent simulations of a system ("replicas") via geometrical distances as well as (ii) probabilistic inference applied to the solutions found by individual replicas. The {\it ensemble} of replicas evolves as to maximize the inter-replica correlation while simultaneously minimize the local intra-replica cost function (e.g., the total path length in the Traveling Salesman Problem within each replica). We demonstrate how our method improves the performance of rudimentary local optimization schemes long applied to the NP hard Traveling Salesman Problem. In particular, we apply our method to the well-known "$k$-opt" algorithm and examine two particular cases- $k=2$ and $k=3$. With the aid of geometrical coupling alone, we are able to determine for the optimum tour length on systems up to $280$ cities (an order of magnitude larger than the largest systems typically solved by the bare $k=3$ opt). The probabilistic replica-based inference approach improves $k-opt$ even further and determines the optimal solution of a problem with $318$ cities and find tours whose total length is close to that of the optimal solutions for other systems with a larger number of cities.
Automatic Segmentation of Fluorescence Lifetime Microscopy Images of Cells Using Multi-Resolution Community Detection
May 08, 2013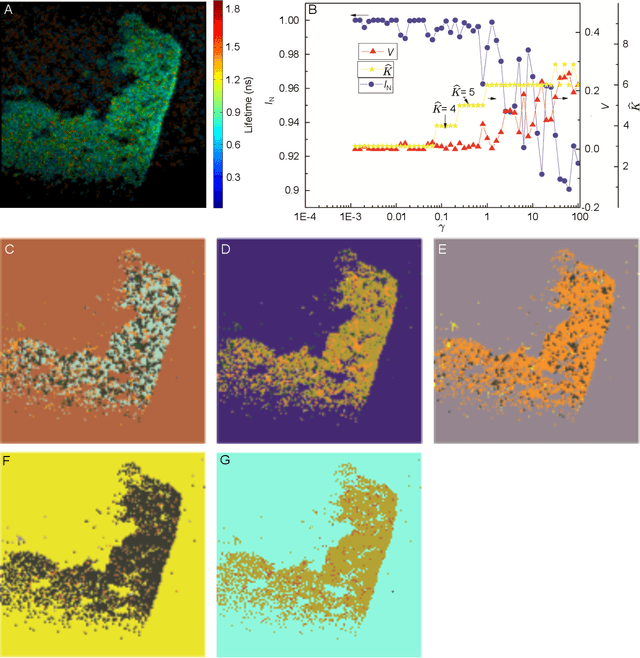


Abstract:We have developed an automatic method for segmenting fluorescence lifetime (FLT) imaging microscopy (FLIM) images of cells inspired by a multi-resolution community detection (MCD) based network segmentation method. The image processing problem is framed as identifying segments with respective average FLTs against a background in FLIM images. The proposed method segments a FLIM image for a given resolution of the network composed using image pixels as the nodes and similarity between the pixels as the edges. In the resulting segmentation, low network resolution leads to larger segments and high network resolution leads to smaller segments. Further, the mean-square error (MSE) in estimating the FLT segments in a FLIM image using the proposed method was found to be consistently decreasing with increasing resolution of the corresponding network. The proposed MCD method outperformed a popular spectral clustering based method in performing FLIM image segmentation. The spectral segmentation method introduced noisy segments in its output at high resolution. It was unable to offer a consistent decrease in MSE with increasing resolution.
* 21 pages, 6 figures
A Replica Inference Approach to Unsupervised Multi-Scale Image Segmentation
Jun 28, 2011



Abstract:We apply a replica inference based Potts model method to unsupervised image segmentation on multiple scales. This approach was inspired by the statistical mechanics problem of "community detection" and its phase diagram. Specifically, the problem is cast as identifying tightly bound clusters ("communities" or "solutes") against a background or "solvent". Within our multiresolution approach, we compute information theory based correlations among multiple solutions ("replicas") of the same graph over a range of resolutions. Significant multiresolution structures are identified by replica correlations as manifest in information theory overlaps. With the aid of these correlations as well as thermodynamic measures, the phase diagram of the corresponding Potts model is analyzed both at zero and finite temperatures. Optimal parameters corresponding to a sensible unsupervised segmentation correspond to the "easy phase" of the Potts model. Our algorithm is fast and shown to be at least as accurate as the best algorithms to date and to be especially suited to the detection of camouflaged images.
* 26 pages, 22 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge